Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(\frac{1}{7}\right)^7.7^7\)=\(\frac{1^7}{7^7}.7^7=1^7=1\)

Ví dụ bảng xét dấu căn bản nhất, phương trình có từ 1 nghiệm trở lên, lập bảng xét dấu như sau:
- Chia bảng thành 2 hàng:
. Hàng 1: x: liệt kê nghiệm theo thứ tự tăng dần.
. Hàng 2: y: thêm số 0 dưới mỗi nghiệm của phương trình,
+ Nếu phương trình ax + b = 0 có 1 nghiệm, hiển nhiên hàng y của bảng xét dấu sẽ có 1 số 0, xét dấu theo quy tắc "trước trái sau cùng" (phía trước số 0, xét dấu ngược với dấu của cơ số a, phía sau số 0 thì cùng dấu với cơ số a)
+ Nếu phương trình ax^2 + bx + c = 0 có 2 nghiệm, hàng y của bảng xét dấu sẽ có 2 số 0, quy tắc xét dấu sẽ là "trong trái ngoài cùng" (giữa 2 số 0, dấu sẽ khác với dấu của cơ số a, và 2 bên trái phải sẽ là dấu cùng với dấu của cơ số a). TRƯỜNG HỢP phương trình trên vô nghiệm HOẶC có nghiệm kép thì tất cả các dấu trong bảng xét dấu sẽ cùng dấu với cơ số a.
+ Nếu phương trình ax^3 + bx^2 + cx + d = 0 có 3 nghiệm, hàng y của bảng xét dấu sẽ có 3 số 0. Theo thứ tự từ phải sang, dấu sẽ được xét dựa trên dấu của cơ số a: cùng, trái, cùng, trái.

1: Xét ΔEAD và ΔBAC có
AE=AB
\(\widehat{EAD}=\widehat{BAC}\)
AD=AC
Do đó: ΔEAD=ΔBAC
SUy ra: ED=BC
2: Xét ΔADC có AD=AC
nên ΔADC cân tại A
Xét ΔAEB có AE=AB
nên ΔAEB cân tại A
3: Ta có: ΔABE cân tại A
mà AM là đường trung tuyến
nên AM là đường cao

Câu 1.
\(M=\left(-\dfrac{2a^3b^2}{3}xy^2z\right)^3.\left(-\dfrac{3}{4}ab^{-3}x^2yz^2\right)^2.\left(-xy^2z^2\right)^2\)
\(=\left(-\dfrac{8}{27}a^9b^6x^3y^6z^3\right).\left(\dfrac{9}{16}a^2b^{-6}x^4y^2z^4\right).\left(x^2y^4z^4\right)\)
\(=-\dfrac{8}{27}.\dfrac{9}{16}.a^{11}x^9y^{12}z^{11}\)
\(=-\dfrac{1}{6}a^{11}x^9y^{12}z^{11}\)
Hệ số: \(-\dfrac{1}{6}\)
Bậc: \(43\)
Câu 2.
a) \(A\left(x\right)=\dfrac{1}{2}x^5+\dfrac{3}{4}x-12x^4-1\dfrac{2}{3}x^3+5+x^2+\dfrac{5}{3}x^3-\dfrac{11}{4}x+1\dfrac{1}{2}x^5+4x\)
\(=\left(\dfrac{1}{2}x^5+\dfrac{3}{2}x^5\right)+\left(-12x^4\right)+\left(-\dfrac{5}{3}x^3+\dfrac{5}{3}x^3\right)+x^2+\left(\dfrac{3}{4}x-\dfrac{11}{4}x+4x\right)+5\)
\(=2x^5-12x^4+x^2+2x+5\)
\(B\left(x\right)=-2x^5+\dfrac{3}{7}x+12x^4-\dfrac{7}{3}x^3-3-6x^2+\dfrac{13}{3}x^3+3\dfrac{4}{7}x\)
\(=\left(-2x^5\right)+12x^4+\left(-\dfrac{7}{3}x^3+\dfrac{13}{3}x^3\right)-6x^2+\left(\dfrac{3}{7}x+\dfrac{25}{7}x\right)-3\)
\(=-2x^5+12x^4+2x^3-6x^2+4x-3\)
b) \(C\left(x\right)=A\left(x\right)+B\left(x\right)=\left(2x^5-12x^4+x^2+2x+5\right)+\left(-2x^5+12x^4+2x^3-6x^2+4x-3\right)\)
\(=\left(2x^5-2x^5\right)+\left(-12x^4+12x^4\right)+2x^3+\left(x^2-6x^2\right)+\left(2x+4x\right)+\left(5-3\right)\)
\(=2x^3-5x^2+6x+2\)
\(D\left(x\right)=A\left(x\right)-B\left(x\right)=\left(2x^5-12x^4+x^2+2x+5\right)-\left(-2x^5+12x^4+2x^3-6x^2+4x-3\right)\)
\(=\left(2x^5+2x^5\right)+\left(-12x^4-12x^4\right)-2x^3+\left(x^2+6x^2\right)+\left(2x-4x\right)+\left(5+3\right)\)
\(=4x^5-24x^4-2x^3+7x^2-2x+8\)
c) \(2x^3-5x^2+6x+2-2x^3+5x^2=-4\)
\(\Rightarrow\left(2x^3-2x^3\right)+\left(-5x^2+5x^2\right)+6x+2\)
\(\Rightarrow6x+2=-4\)
\(\Rightarrow6x=-6\)
\(\Rightarrow x=-1\)
Câu 3.
1) \(M-3xy^2+2xy-x^3+2x^2y=2xy-3x^3+3x^2y-xy^2\)
\(\Rightarrow M=\left(3xy^2+2xy-x^3+2x^2y\right)+\left(2xy-3x^3+3x^2y-xy^2\right)\)
\(=\left(3xy^2-xy^2\right)+\left(2xy+2xy\right)+\left(-x^3-3x^3\right)+\left(2x^2y+3x^2y\right)\)
\(=2xy^2+4xy-4x^3+5x^2y\)
2)
Để cho \(f\left(x\right)\) có nghiệm thì \(6-3x=0\)
\(\Rightarrow3x=6\)
\(\Rightarrow x=2\)
Để cho \(g\left(x\right)\) có nghiệm thì \(x^2-1=0\)
\(\Rightarrow x^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

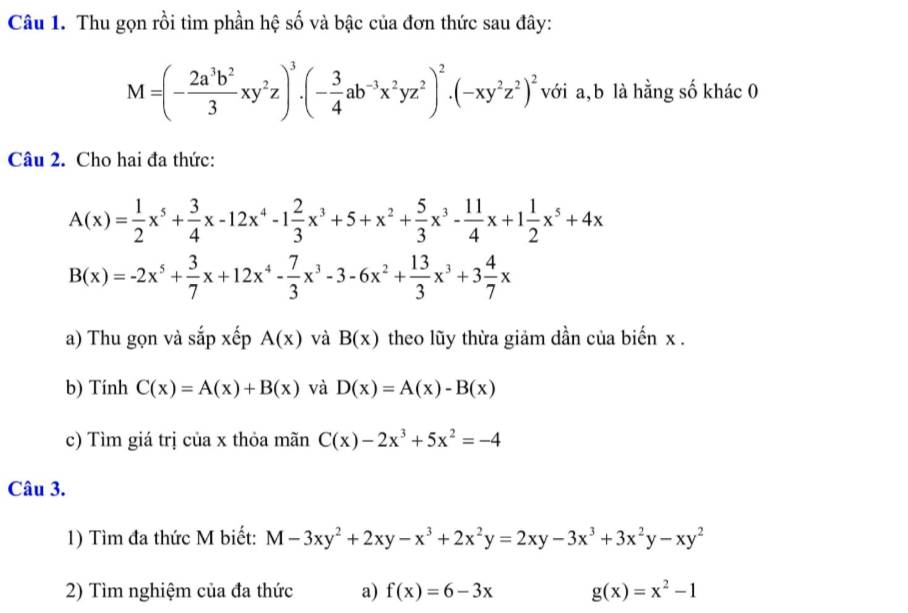
không nghe thầy cô giảng là một cái tội
ví dụ : 3,453653767=3,5 lảm tròn đến số thứ nhất sau dấu phảy