Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

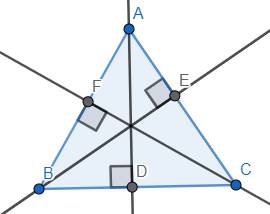
Nhận xét: AD, BE và CF là các đường cao, chúng đồng quy tại một điểm.
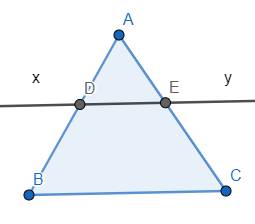
Dễ dàng thấy được \(\widehat{ABC}=\widehat{ADE}\) và \(\widehat{ACB}=\widehat{AED}\) (vì với mỗi cặp thì hai góc của cặp đó là hai góc so le trong)
Vì \(\widehat{ADE}\) và \(\widehat{BDE}\) là hai góc kề bù nên \(\widehat{ADE}+\widehat{BDE}=180^o\)
Mà \(\widehat{ABC}=\widehat{ADE}\) nên \(\widehat{ABC}+\widehat{BDE}=180^o\), suy ra \(\widehat{ABC}\) và \(\widehat{BDE}\) là hai góc bù nhau.
Suy luận tương tự như trên, ta được \(\widehat{ACB}\) và \(\widehat{CED}\) là hai góc bù nhau.

\(\widehat{ADE}=\widehat{ABC}\) (góc đồng vị)
\(\widehat{AED}=\widehat{ACB}\) (góc đồng vị)
\(\widehat{ABC}+\widehat{BDE}=180^o\) (hai góc trong cùng phía bù nhau)
\(\widehat{ACB}+\widehat{CED}=180^o\) (hai góc trong cùng phía bù nhau)
\(\widehat{ABC}=\widehat{BDx}\) (góc sole trong)
\(\widehat{ACB}=\widehat{CEy}\) (góc sole trong)