
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

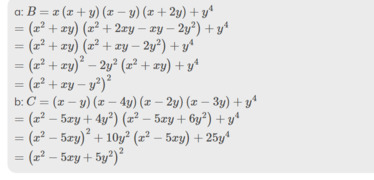

a: \(B=x\left(x+y\right)\left(x-y\right)\left(x+2y\right)+y^4\)
\(=\left(x^2+xy\right)\left(x^2+2xy-xy-2y^2\right)+y^4\)
\(=\left(x^2+xy\right)\left(x^2+xy-2y^2\right)+y^4\)
\(=\left(x^2+xy\right)^2-2y^2\left(x^2+xy\right)+y^4\)
\(=\left(x^2+xy-y^2\right)^2\)
b: \(C=\left(x-y\right)\left(x-4y\right)\left(x-2y\right)\left(x-3y\right)+y^4\)
\(=\left(x^2-5xy+4y^2\right)\left(x^2-5xy+6y^2\right)+y^4\)
\(=\left(x^2-5xy\right)^2+10y^2\left(x^2-5xy\right)+25y^4\)
\(=\left(x^2-5xy+5y^2\right)^2\)

Bài 1:
A=x2 +y2 -2x-2y+2xy+5
=x2 +y2 -2x-2y+2xy+1+4
=xy+x2-x+xy+y2-y-y-x+1+4
=x(x+y-1)+y(x+y-1)-1(x+y-1)
=(x+y-1)(x+y-1)
=(x+y-1)2+4.Với x+y=3
=>A=(3-1)2+4=22+4=8
Bài 2:
B=x^2 +4y^2-2x-4y-4xy+10
=-2xy+x2-x-2xy+4y2+2y-x+2y+1-8y+9
=x(x-2y-1)-2y(x-2y-1)-1(x-2y-1)-8y+9
=(x-2y-1)(x-2y-1)-8y+9
=(x-2y-1)2-8y+9
Với x-2y=5.Ta có:... tự thay
Bài 3: chịu

Ta có \(A=\left(x+y\right)\left(x+2y\right)\left(x+3y\right)\left(x+4y\right)+y^4\)
\(=\left(x^2+5xy+4y^2\right)\left(x^2+5xy+6y^2\right)+y^4\)
Đặt \(x^2+5xy+5y^2=t\) thì:
\(A=\left(t-y^2\right)\left(t+y^2\right)+y^4=t^2-y^4+y^4=t^2=\left(x^2+5xy+5y^2\right)^2\)
Vì \(x,y\in Z\) nên \(x^2\in Z,\)\(5xy\in Z,\)\(5y^2\in Z\)\(\Rightarrow\)\(x^2+5xy+5y^2\in Z\)
Vậy A là số chính phương.

Bài 2:
a: \(3x^2-3xy=3x\left(x-y\right)\)
b: \(x^2-4y^2=\left(x-2y\right)\left(x+2y\right)\)
c: \(3x-3y+xy-y^2=\left(x-y\right)\left(3+y\right)\)
d: \(x^2-y^2+2y-1=\left(x-y+1\right)\left(x+y-1\right)\)

a, (\(x\) + y).(\(x\) + y)2 - 3\(xy\).(\(x\) + y)
= (\(x+y\))3 - 3\(x^2\)y - 3\(xy^2\)
= \(x^3\) + 3\(x^2\).y + 3\(xy^2\) + y3 - 3\(x^2\).y - 3\(xy^2\)
= \(x^3\) + y3
b, (\(x-y\)).(\(x-y\))2 - 3\(xy\).(\(x-y\))
= (\(x\) - y)3 - 3\(x^2\).y + 3\(xy^2\)
= \(x^3\) - 3\(x^2\)y + 3\(xy^2\) - y3 - 3\(x^2\)y + 3\(xy^2\)
= \(x^3\) - 6\(x^2\)y + 6\(xy^2\) - y3

\(\text{a) }\left(x-1\right)\left(x^2+y\right)-\left(x^2-y\right)\left(x-2\right)-x\left(x+2y\right)+3\left(y-5\right)\)
\(=\left(x^3+xy-x^2-y\right)-\left(x^3-2x^2-xy+2y\right)-\left(x^2+2xy\right)+\left(3y-15\right)\)
\(=x^3+xy-x^2-y-x^3+2x^2+xy-2y-x^2-2xy+3y-15\)
\(=\left(x^3+x^3\right)+\left(-x^2+2x^2-x^2\right)+\left(xy+xy-2xy\right)+\left(-y-2y+3y\right)-15\)
\(=0+0+0+0-15\)
\(=-15\)
\(\text{b) }6\left(x^3y+x-3\right)-6x\left(2xy^3+1\right)-3x^2y\left(2x-4y^2\right)\)
\(=\left(6x^3y+6x-18\right)-\left(12x^2y^3+6x\right)-\left(6x^3y-12x^2y^3\right)\)
\(=6x^3y+6x-18-12x^2y^3-6x-6x^3y+12x^2y^3\)
\(=\left(6x^3y-6x^3y\right)+\left(6x-6x\right)+\left(-12x^2y^3+12x^2y^3\right)-18\)
\(=0+0+0-18\)
\(=-18\)
\(\text{c) }\left(x^2+2xy+4y^2\right)\left(x-2y\right)-6\left(\frac{1}{2}-\frac{4}{3}y^3\right)\)
\(=\left(x^3-2x^2y+2x^2y-4xy^2+4xy^2-8y^3\right)-\left(3-8y^3\right)\)
\(=\left(x^3-8y^3\right)-\left(3-8y^3\right)\)
\(=x^3-8y^3-3+8y^3\)
\(=x^3-3\)