Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEDF có
AE//DF
DE//AF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
a, Vì DE//AB nên DE⊥AC và DF//AC nên DF⊥AB
Vì \(\widehat{AED}=\widehat{AFD}=\widehat{EAF}=90^0\) nên AEDF là hcn
b,Vì E là trung điểm MD và AC nên AMCD là hbh
Mà AC⊥DE nên AMCD là hthoi
c, Vì D là trung điểm BC và AK và \(\widehat{BAC}=90^0\) nên ABKC là hcn
Để ABKC là hv thì AB=AC hay tam giác ABC vuông cân tại A

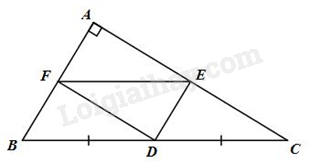
a) Ta có:
\(\Delta ABC\) vuông tại \(A\) nên \(\widehat {{\rm{BAC}}} = 90^\circ \) và \(AB \bot AC\)
Mà \(DE\) // \(AB\) ; \(DF\) // \(AC\)
Suy ra \(DE \bot AC;\;DF \bot AB\)
Suy ra \(\widehat {DEA} = \widehat {DFA} = 90^\circ \)
Tứ giác \(AEDF\) có \(\widehat {BAC} = \widehat {DEA} = \widehat {DFA} = 90^\circ \) nên là hình chữ nhật
b) Vì \(AEDF\) là hình chữ nhật (cmt)
Suy ra \(AE = DF\); \(AF = DE\); \(AF\) // \(DE\); \(AE\) // \(DF\)
Vì \(DE \bot AC;\;DF \bot AB\) (cmt)
Suy ra \(\widehat {DEC} = \widehat {BFD} = 90^\circ \)
Xét \(\Delta BFD\) và \(\Delta DEC\) ta có:
\(\widehat {{\rm{BFD}}} = \widehat {{\rm{DEC}}} = 90^\circ \) (cmt)
\(BD = DC\) (gt)
\(\widehat {{\rm{FBD}}} = \widehat {{\rm{EDC}}}\) (do \(DE\) // \(BF\) )
Suy ra \(\Delta BFD = \Delta DEC\) (ch – gn)
Suy ra \(BF = DE\); \(DF = EC\) (hai cạnh tương tứng)
Xét tứ giác \(BFED\) ta có:
\(BF\) // \(DE\) (do \(AB\) // \(DE\))
\(BF = DE\) (cmt)
Suy ra \(BFED\) là hình bình hành

Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành

a) vận dụng định lý của lớp 6. DE//AB VÀ AB \(\perp\) AC => DE \(\perp\) AC
TƯƠNG TỰ DF \(\perp\) AB
=> HCN (3 GÓC VUÔNG)
b) vận dụng định lý đường trung bình => E là trung điểm của AC
=> DE = 1/2 AB = BF
=> BFED là HBH (1 cặp cạnh đối // và = nhau)

Bài 1 : Ta có MB = MC ( gt) , ME // AC => E là trung điểm của AB ( đường thẳng qua trung điểm cạnh tam giác . . )
MB = MC ( gt) , MF // AB ⇒ F là trung điểm của AC ( đường thẳng qua trung điểm cạnh tam giác . . . )
⇒ EF là đường trung bình của tam giác ABC . ⇒ EF // BC Vậy tứ giác BCEF là hình thang
. Mặt khác góc B = góc C ( tam giác ABC cân – gt) ⇒ Tứ giác BCEF là hình thang cân.
Bài 2: a/ chứng minh tứ giác có 2 cặp cạnh đối song song ( gt) nên AEGF là hình bình hành.
tứ giác có góc A = 900 ( gt)
Vậy AEGF là hình chữ nhật
b/ vì GF // AB ⇒ FI // EB
EI // BF (gt) ⇒ BEIF là hình bình hành ( 2 cặp cạnh đối // )
c/ Vì AF = FC , GB = GC ( gt) ⇒ GF là đường trung bình của tam giác ABC ⇒ GF = BE = 1/2 AB ⇒ GF = FI ( vì FI = BE do BEIF là hình bình hành)
⇒ GF // AB mà AB ⊥ AC ⇒ GI ⊥ AC tại F
Vậy AGCI là hình thoi ( hai đ/chéo vuông góc tại trung điểm mỗi đường )
d/ Để AGCI là hình vuông thì AC = GI . mà GI = 2GF = 2 EB = AB Vậy AGCI là hình vuông thì AC = AB ⇒ Tam giác ABC vuông cân tại A.

Bài 2:
a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trug điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: Để AMCK là hình vuông thì AM=CM
=>AM=BC/2
=>ΔABC vuông tại A
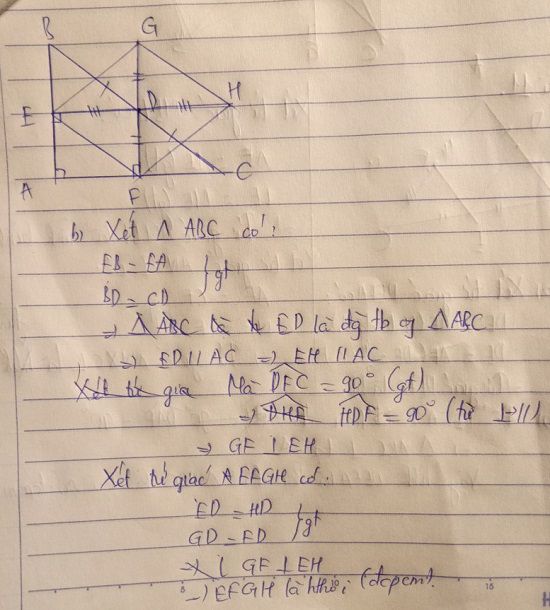

a/
DE//AB=> DE//AF
DF//AC=>DF//AE
=> AEDF là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Hình bình hành AEDF có \(\widehat{A}=90^o\) => AEDF là hình chữ nhật
b/
DE//AB
DB=DC (1)
=> FA=FC (trong tg đường thẳng đi qua trung điểm 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại (2)
Từ (1) và (2) => DE là đường trung bình của ABC
\(\Rightarrow DE=\dfrac{BC}{2}=FB=FC\) (3)
DE//AB=> DE//FB (4)
Từ (3) và (4) => BFED là hình bình hành (Tứ giác có cặp cạnh đối // và bằng nhau là hbh)
a) Do DE // AB (gt)
\(AC\perp AB\) (\(\Delta ABC\) vuông tại A)
\(\Rightarrow DE\perp AC\)
\(\Rightarrow\widehat{DEA}=90^0\)
Do DF // AC (gt)
\(AB\perp AC\) (\(\Delta ABC\) vuông tại A)
\(\Rightarrow DF\perp AC\)
\(\Rightarrow\widehat{DFA}=90^0\)
Tứ giác AEDF có:
\(\widehat{EAF}=\widehat{DEA}=\widehat{DFA}=90^0\)
\(\Rightarrow AEDF\) là hình chữ nhật
b) Do D là trung điểm BC (gt)
DF // AB (gt)
\(\Rightarrow F\) là trung điểm của AB
\(\Rightarrow FA=FB\)
Do AEDF là hình bình hành
\(\Rightarrow DE=AF\)
\(\Rightarrow DE=FB\)
Lại có:
DE // AB
\(\Rightarrow\) DE // FB
Tứ giác BFED có:
DE // FB (cmt)
DE = FB (cmt)
\(\Rightarrow BFED\) là hình bình hành