b) Cho M = 2014 100 - 2014 99 và N = 2014 99

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

22 tháng 9 2019

b) Cho M = 2014 100 - 2014 99 và N = 2014 99 - 2014 98 . Hãy so sánh M và N

#Toán lớp 6

Cao Minh Tâm

22 tháng 9 2019

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PHAN QUỐC VIỆT HƯNG

18 tháng 7 2015 - olm

Cho a=2014¹⁰⁰-2014⁹⁹và b= 2014⁹⁹-2014⁹⁸ so sánh a và b

#Toán lớp 6

doremon

18 tháng 7 2015

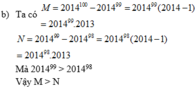
a = 2014¹⁰⁰- 2014⁹⁹= 2014⁹⁹(2014 - 1) = 2014⁹⁹.2013

b = 2014⁹⁹- 2014⁹⁸= 2014⁹⁸(2014 - 1) = 2014⁹⁸.2013

Vì 2014⁹⁹.2013 > 2014⁹⁸.2013 => a > b

Đúng(0)

Trần Đức Thắng

18 tháng 7 2015

A= 2014^100 - 2014^99 = 2014^99 ( 2014 -1) = 2014^99 . 2013

B = 2014^99 - 2014^98 = 2014^98 ( 2014 - 1) = 2013.2014^98

Vì 2014^98 <2014^99 > 2013.2014^98 < 2013.2014^99

=> B < A

Đúng(0)

Lê Khánh Huyền

11 tháng 4 2017 - olm

a, Cho A=\(\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+\frac{1}{14}+...+\frac{1}{99}+\frac{1}{100}\) . So Sánh A với 1b, B=\(\frac{1}{11}+\frac{1}{12}+...+\frac{1}{20}\). So sánh B với \(\frac{1}{2}\)c, cho M=\(\frac{2013}{2014}+\frac{2014}{2015}\)và N=\(\frac{2013+2014}{2014+2015}\). So sánh M và NCâu a, p/s cuối cùng là \(\frac{1}{100}\)nha mí...

Đọc tiếp

#Toán lớp 6

trần phương uyên

11 tháng 4 2017

kb đc 0

Đúng(0)

Nguyễn Thị Thu Huyền

11 tháng 4 2017

2 câu đầu tôi làm đc

Đúng(0)

Horikita Suzune

18 tháng 4 2018 - olm

GIÚP MÌNH VỚI CÁC BẠN ƠI !

BÀI 1:

Cho A =1/5+1/5^2+1/5^3+...+1/5^99+1/5^100

a.Tính A?

So sánh A với 1/4

BÀI 2 :

So sánh :

a. A=9/a^2014+7/a^2014 và B=8/a^2014+8/a^2013 với A thuộc N*

b . So sánh A và B với A=10^2009+1/10^2010+1 và B=10^2010+1/10^2011+1

c . So sánh A=10^2016+1/ 10^2015+1 ; B=10^2015+1/10^2014+1

#Toán lớp 6

Phan Nghĩa

10 tháng 5 2021

a,\(A=\frac{1}{5}+\frac{1}{5^2}+\frac{1}{5^3}+...+\frac{1}{5^{100}}\)

\(=>5A=1+\frac{1}{5}+\frac{1}{5^2}+...+\frac{1}{5^{99}}\)

\(=>5A-A=1-\frac{1}{5^{100}}=>A=\frac{1-\frac{1}{5^{100}}}{4}\)

b, Ta có \(1-\frac{1}{5^{100}}< 1=>\frac{1-\frac{1}{5^{100}}}{4}< \frac{1}{4}\)hay \(A< \frac{1}{4}\)

Đúng(0)

Nguyễn Bích Diệu

27 tháng 3 2018 - olm

so sánh 2 phân số sau :

A= \(\frac{99^{2015}+1}{99^{2014}+1}\) và B= \(\frac{99^{2014}+1}{99^{2013}+1}\)

#Toán lớp 6

Phùng Minh Quân

28 tháng 3 2018

Ta có công thức :

\(\frac{a}{b}>\frac{a+c}{b+c}\)\(\left(\frac{a}{b}>1;a,b,c\inℕ^∗\right)\)

\(A=\frac{99^{2015}+1}{99^{2014}+1}>\frac{99^{2015}+1+98}{99^{2014}+1+98}=\frac{99^{2015}+99}{99^{2014}+99}=\frac{99\left(99^{2014}+1\right)}{99\left(99^{2013}+1\right)}=\frac{99^{2014}+1}{99^{2013}+1}=B\)

\(\Rightarrow\)\(A>B\)

Chúc bạn học tốt ~

Đúng(0)

Phí Quỳnh Anh

16 tháng 5 2016 - olm

So sánh: M=(2014 mũ 2014)+1 phần( 2014 mũ 2015)+1 và N=(2014 mũ 2004)+1 phần( 2014 mũ 2025)+1

#Toán lớp 6

Phan Văn Tài

30 tháng 3 2016 - olm

Cho M=\(\frac{2013}{2014}+\frac{2014}{2015}\)

N=\(\frac{2013+2014}{2014+2015}\)

So sánh M và N

#Toán lớp 6

Tiểu Sam Sam

30 tháng 3 2016

Ta có:

\(\frac{2013}{2014}>\frac{2013}{2014+2015}\)

\(\frac{2014}{2015}>\frac{2014}{2014+2015}\)

\(\Rightarrow\frac{2013}{2014}+\frac{2014}{2015}>\frac{2013+2014}{2014+2015}\)

\(\Rightarrow M>N\)

Đúng(0)

Real Madrid

30 tháng 3 2016

Ta có: \(N=\frac{2013+2014}{2014+2015}<1\);

\(M=\frac{2013}{2014}+\frac{2014}{2015}>\frac{2013}{2015}+\frac{2014}{2015}=\frac{4027}{2015}>1\)

\(\Rightarrow A>B\)

Đúng(0)

tranthihuyen

3 tháng 4 2017 - olm

a, so sánh

M=2013/2014+2014/2015 va N=2013+2014/2014+2015

b, tìm số tự nhiên n sao cho n+3 chia hết cho n^2+1

#Toán lớp 6

Mạc Thị Thu Hiền

16 tháng 4 2016 - olm

So sánh M = \(\frac{2014}{1.2.3}+\frac{2014}{2.3.4}+\frac{2014}{3.4.5}+.....+\frac{2014}{2012.2013.2014}\) và N= 2013

#Toán lớp 6

Nguyễn Hữu Huy

16 tháng 4 2016

ta xét vế M

đầu tiên bạn tách 2014 ra ngoài

sau đó nhân 2 vào tử và mẫu , rồi tách 1/2 ra ta có 1007 .( ..........................)

bây giờ tính vế trong ngoặc và trong ngoặc <1

=> M>N

Đúng(0)

pham ngoc yen nhi

16 tháng 1 2020 - olm

bài 1cho E=\(\frac{2018^{99^{ }}-1}{2018^{100}-1}\) và F=\(\frac{2018^{98}-1}{2018^{99}-1}\) .hãy so sánh E và Fbài 2cho tổng gồm 2014 số hạng:S=\(\frac{1}{4}\)+\(\frac{2}{4^2}^{ }\)+\(\frac{3}{4^3}\)+\(\frac{4}{4^4}\)+......+\(\frac{2014}{4^{2014}}\).Chứng minh rằng : S<\(\frac{1}{2}\)bạn nào làm vừa chuẩn vừa nhanh thì được nhiều tik nha...

Đọc tiếp

#Toán lớp 6

Hoàng Thanh Hà

27 tháng 1 2016 - olm

1. So sánh M và N ( Ko Quy Đồng)

biết M = \(\frac{2012}{2013}+\frac{2013}{2014}+\frac{2014}{2015}\)và

N =\(\frac{2012+2013+2014}{2013+2014+2015}\)

( Giải rõ ràn nha) tớ tick cho

#Toán lớp 6

Mai Ngọc

27 tháng 1 2016

\(N=\frac{2012+2013+2014}{2013+2014+2015}=\frac{2012}{2013+2014+2015}+\frac{2013}{2013+2014+2015}+\frac{2014}{2013+2014+2015}\)

Ta thấy: \(\frac{2012}{2013}>\frac{2012}{2013+2014+2015}\)

\(\frac{2013}{2014}>\frac{2013}{2013+2014+2015}\)

\(\frac{2014}{2015}>\frac{2014}{2013+2014+2015}\)

\(\Rightarrow M=\frac{2012}{2013}+\frac{2013}{2014}+\frac{2014}{2015}>N=\frac{2012}{2013+2014+2015}+\frac{2013}{2013+2014+2015}+\frac{2014}{2013+2014+2015}\)

Vậy M>N

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP