Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(A=\dfrac{1}{2}QU\)
Công tổng cộng để tích điện cho tụ từ trạng thái ban đầu đến khi có điện tích Q là năng lượng được dự trữ trong tụ điện dưới dạng năng lượng điện trường.
Và Q=CU nên thay vào công thức trên ta thu được:
\(W=\dfrac{1}{2}QU=\dfrac{1}{2}CU^2=\dfrac{Q^2}{2C}\)

Từ các công thức (13.5), (13.6) và (13.7), ta có:
\(U_{AB}=V_A-V_B=\dfrac{A_{A\infty}}{q}-\dfrac{A_{B\infty}}{q}=\dfrac{A_{A\infty}-A_{B\infty}}{q}\)
Mà: \(A_{A\infty}=A_{AB}+A_{B\infty}\)
\(\Rightarrow U_{AB}=\dfrac{A_{AB}+A_{B\infty}-B_{B\infty}}{q}=\dfrac{A_{AB}}{q}\)

Hiệu điện thế UMN bằng độ biến thiên thế năng từ M đến N: UMN = VM - VN
\({V_{MN}} = \frac{{{A_{MN}}}}{q}\) ⇒ ANM = (VM−VN)q = UMN.q

Bước sóng \(\lambda \)là quãng đường mà sóng truyền đi được trong một chu kì sóng T.
Tốc độ của sóng v là tốc độ lan truyền của sóng trong không gian.
Do đó: \(v = \frac{\lambda }{T}\)(1).
Tần số sóng f là số dao động mà mỗi điểm sóng thực hiện trong một đơn vị thời gian.
\(f = \frac{1}{T}\)(2).
Từ (1)(2) suy ra \(v = \lambda f\)(đpcm).

Công thức (3.5): \(W_d=\dfrac{1}{2}mw^2A^2sin^2\left(wt+\varphi_0\right)\)
Đồ thị động năng – thời gian cũng có dạng hình sin.
Từ đồ thị ta thấy:
+ Tại thời điểm ban đầu, động năng bằng 0
+ Tại thời điểm \(\dfrac{T}{4}\), động năng cực đại
+ Tại thời điểm \(\dfrac{T}{2}\), động năng bằng 0
+ Tại thời điểm \(\dfrac{3T}{4}\), động năng cực đại
+ Tại thời điểm T, động năng bằng 0.

Tham khảo:
Từ công thức \(I=\dfrac{\Delta q}{\Delta t}\), ta thấy cường độ dòng điện được định nghĩa thông qua tỉ số giữa điện lượng dịch chuyển qua tiết diện thẳng và khoảng thời gian để thực hiện sự dịch chuyển đó.
Trong chương trình môn Khoa học tự nhiên 8, các em đã được học đơn vị của cường độ dòng điện trong hệ SI (A) đơn được chọn là đơn vị cơ bản, do đó đơn vị của điện tích (C) được định nghĩa lại như sau: 1 culông (1 C) là điện lượng chuyển qua tiết diện thẳng của dây dẫn trong 1 s khi có dòng điện không đổi cường độ 1 A chạy qua.
1C= 1A.1s = 1As

Từ hình 26.1, áp dụng định luật khúc xạ ta có:
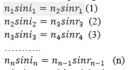
Vì các mặt phân cách sóng song với nhau nên:
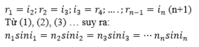

Thế năng của vật đạt giá trị lớn khi ở vị trí hai biên và đạt giá trị nhỏ nhất ở vị trí cân bằng khi vật di chuyển từ vị trí biên đến vị trí cân bằng thế năng của vật giảm dần từ giá trị lớn nhất về 0 và ngược lại.

Công thức 19.2:
\(W_M=A_{M\infty}\)
Công thức 19.3:
\(W_M=V_Mq\)
Điện thế tại điểm M:
\(V_M=\dfrac{W_M}{q}=\dfrac{A_{M\infty}}{q}\) và \(V=\dfrac{A}{q}\)

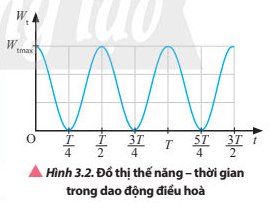
Độ biến thiên động năng bằng công của lực điện trường:
\({W_d} - {W_{d0}} = A \Rightarrow \frac{1}{2}m{v^2} - 0 = {q_e}Ed \Rightarrow v = \sqrt {\frac{{2{q_e}Ed}}{m}} \)