
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: EC//AB
AB⊥CD
Do đó: EC⊥CD
=>ΔCED nội tiếp đường tròn đường kính CD
=>O là trung điểm của CD(Vì C,E,D cùng nằm trên đường tròn O)
=>E,O,D thẳng hàng
b: Xét (O) có
ΔAEB nội tiếp
AB là đường kính
DO đó: ΔAEB vuông tại E
Xét tứ giác AEBD có
O là trung điểm của AB
O là trung điểm của ED
Do đó: AEBD là hình bình hành
mà \(\widehat{AEB}=90^0\)
nên AEBD là hình chữ nhật

R=1/2CD=a
h=AD=2a
S1=Sxq=2*pi*r*h=2*pi*a*2a=4*pi*a^2
S2=Stp=2*pi*r^2+2*pi*r*h
=2*pi*a^2+2*pi*a*2a
=6*pi*a^2
>S1/S2=2/3

a: Δ=(m-2)^2-4(m-4)
=m^2-4m+4-4m+16
=m^2-8m+20
=m^2-8m+16+4
=(m-2)^2+4>=4>0
=>Phương trình luôn có 2 nghiệm pb
b: x1^2+x2^2
=(x1+x2)^2-2x1x2
=(m-2)^2-2(m-4)
=m^2-4m+4-2m+8
=m^2-6m+12
=(m-3)^2+3>=3
Dấu = xảy ra khi m=3

a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2

\(\sqrt{a^2+3}=\sqrt{a^2+ab+bc+ca}=\sqrt{\left(a+b\right)\left(a+c\right)}\le\dfrac{1}{2}\left(a+b+a+c\right)=\dfrac{1}{2}\left(2a+b+c\right)\)
Tương tự: \(\sqrt{b^2+3}\le\dfrac{1}{2}\left(a+2b+c\right)\) ; \(\sqrt{c^2+3}\le\dfrac{1}{2}\left(a+b+2c\right)\)
Cộng vế với vế:
\(VT\le\dfrac{1}{2}\left(4a+4b+4c\right)=2\left(a+b+c\right)\)


1.theo bất đẳng thức côsi ta có
\(a+b\ge2\sqrt{ab}\\ b+c\ge2\sqrt{ab}\\ c+a\ge2\sqrt{ab}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8\sqrt{ab.bc.ca}\)
\(\ge8\sqrt{a^2b^2c^2}\\ \ge8abc\)
2.\(a^4+b^2\ge2\sqrt{a^4b^2}=2a^4b^2\)
\(\dfrac{a}{a^4+b^2}\le\dfrac{a}{2a^2b}=\dfrac{1}{2ab}\)
tương tự:\(\dfrac{b}{b^4+a^2}\le\dfrac{1}{2ab}\)
\(\rightarrow\dfrac{a}{a^4+b^2}+\dfrac{b}{b^4+a^2}\le\dfrac{1}{ab}\)
dấu = xảy ra khi \(a^4=b^2\\ b^4=a^2\)\(\rightarrow a^2=b^2=1\)

Bài 1:
a)
\(A=\left(\frac{4\sqrt{x}}{\sqrt{x}+2}-\frac{8x}{(\sqrt{x}-2)(\sqrt{x}+2)}\right):\left(\frac{\sqrt{x}-1}{\sqrt{x}(\sqrt{x}-2)}-\frac{2(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}\right)\)
\(=\frac{4\sqrt{x}(\sqrt{x}-2)-8x}{(\sqrt{x}-2)(\sqrt{x}+2)}:\frac{\sqrt{x}-1-2(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}=\frac{-4x-8\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{\sqrt{x}(\sqrt{x}-2)}{-\sqrt{x}+3}\)
\(=\frac{-4\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{\sqrt{x}(\sqrt{x}-2)}{3-\sqrt{x}}=\frac{-4x(\sqrt{x}-2)}{(\sqrt{x}-2)(3-\sqrt{x})}=\frac{4x}{\sqrt{x}-3}\)
b)
Ta có:
\(m(\sqrt{x}-3).A>x+2025\)
\(\Leftrightarrow 4xm>x+2025\Leftrightarrow x(4m-1)>2025\)
\(\Leftrightarrow 4m-1>\frac{2025}{x}\Leftrightarrow m>\frac{1}{4}(\frac{2025}{x}+1)\) với mọi $x>9$
\(\Leftrightarrow m> \max \frac{1}{4}(\frac{2025}{x}+1), \forall x>9\Leftrightarrow m>56,5\)




 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
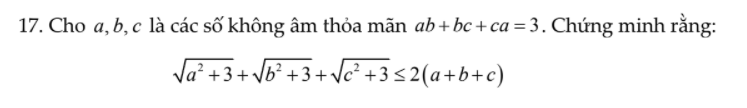 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn.
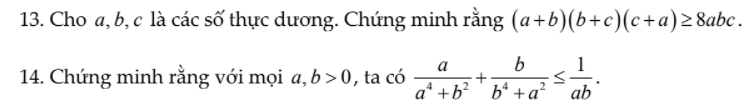



a: Ta có: EC//AB
AB⊥CD
Do đó: EC⊥CD
=>ΔCED nội tiếp đường tròn đường kính CD
=>O là trung điểm của CD(Vì C,E,D cùng nằm trên đường tròn O)
=>E,O,D thẳng hàng
b: Xét (O) có
ΔAEB nội tiếp
AB là đường kính
DO đó: ΔAEB vuông tại E
Xét tứ giác AEBD có
O là trung điểm của AB
O là trung điểm của ED
Do đó: AEBD là hình bình hành
mà \(\widehat{AEB}=90^0\)
nên AEBD là hình chữ nhật