Question

[minh hue]

Ai giúp tui 3 bài này vơi :( 

Answer 1

[Nguyễn Việt Lâm]

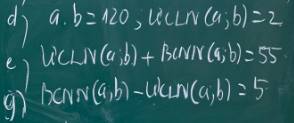
4.

\(\dfrac{x-7}{y-6}=\dfrac{7}{6}\Rightarrow\dfrac{x-7}{7}=\dfrac{y-6}{6}=\dfrac{-y+6}{-6}\)

Áp dụng tính chất dãy tỉ số bằng nhau:

\(\dfrac{x-7}{7}=\dfrac{-y+6}{-6}=\dfrac{x-7-y+6}{7-6}=\dfrac{x-y-1}{1}=-5\)

\(\Rightarrow\left\{{}\begin{matrix}x-7=7.\left(-5\right)=-35\\-y+6=\left(-6\right).\left(-5\right)=30\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=-28\\y=-24\end{matrix}\right.\)

5.

Ta có:

\(A^2=\dfrac{2^2.4^2.6^2...4998^2.5000^2}{3^2.5^2.7^2...4999^2.5001^2}< \dfrac{2^2.4^2.6^2.4998^2.5000^2}{\left(3^2-1\right)\left(5^2-1\right)\left(7^2-1\right)...\left(4999^2-1\right)\left(5001^2-1\right)}\)

\(\Rightarrow A^2< \dfrac{2^2.4^4.6^2...4998^2.5000^2}{2.4.4.6.6.8...4998.5000.5000.5002}=\dfrac{2^2.4^4.6^2...4998^2.5000^2}{2.4^4.6^2...4998^2.5000^2.5002}\)

\(\Rightarrow A^2< \dfrac{2}{5002}=\dfrac{1}{2501}< \dfrac{1}{2500}\)

\(\Rightarrow A< \dfrac{1}{50}\)

\(\Rightarrow A< 0,02\)

Answer 2

[HT.Phong (9A5)]

Bài 3: 

\(A=B\) khi:

\(\dfrac{7}{y-2}=x+1\left(y\ne2\right)\)

\(\Rightarrow\left(x+1\right)\left(y-2\right)=7\)

Mà: x,y nguyên \(\Rightarrow x+1,y-2\inƯ\left(7\right)=\left\{1;-1;7;-7\right\}\) 

Ta có bảng sau: 

x + 1	1	-1	7	-7
y - 2	7	-7	1	-1
x	0	-2	6	-8
y	9	-5	3	1