
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
Theo tính chất lập phương, \(CC'\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của \(AC'\) lên (ABCD)
\(\Rightarrow\widehat{C'AC}\) là góc giữa AC' và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=4\sqrt{2}\)
\(\Rightarrow tan\widehat{C'AC}=\dfrac{CC'}{AC}=\dfrac{1}{\sqrt{2}}\Rightarrow\widehat{C'AC}\approx35^016'\)
b.
Theo t/c lập phương, \(CD\perp\left(BCB'\right)\)
Mà CD là giao tuyến (A'B'CD) và (ABCD)
\(\Rightarrow\widehat{BCB'}\) là góc giữa (A'B'CD) và (ABCD)
\(tan\widehat{BCB'}=\dfrac{BB'}{BC}=\dfrac{4}{4}=1\Rightarrow\widehat{BCB'}=45^0\)
c.
\(AA'\perp\left(A'B'C'D'\right)\Rightarrow AA'\perp A'P\Rightarrow\Delta MA'P\) vuông tại A'
\(\Rightarrow MP=\sqrt{A'M^2+A'P^2}=\sqrt{A'M^2+A'D'^2+D'P^2}\)
\(=\sqrt{2^2+4^2+2^2}=2\sqrt{6}\left(cm\right)\)
Tương tự:
\(MN=\sqrt{AM^2+AB^2+BN^2}=2\sqrt{6}\left(cm\right)\)
\(NP=\sqrt{C'P^2+C'C^2+CN^2}=2\sqrt{6}\left(cm\right)\)
\(\Rightarrow MN=MP=NP\Rightarrow\Delta MNP\) đều
\(\Rightarrow S_{\Delta MNP}=\dfrac{MN^2\sqrt{3}}{4}=6\sqrt{3}\left(cm^2\right)\)
d.
Gọi Q là trung điểm CD \(\Rightarrow PQ\perp\left(ABCD\right)\)
\(\Rightarrow\Delta ANQ\) là hình chiếu vuông góc của tam giác MNP lên (ABCD)
\(S_{\Delta ANQ}=S_{ABCD}-S_{ADQ}-S_{ABN}-S_{CNQ}\)
\(=AB^2-\dfrac{1}{2}AD.DQ-\dfrac{1}{2}AB.BN-\dfrac{1}{2}CQ.CN\)
\(=4^2-\dfrac{1}{2}.4.2-\dfrac{1}{2}.4.2-\dfrac{1}{2}.2.2=6\left(cm^2\right)\)
\(\Rightarrow cos\alpha=\dfrac{S_{AQN}}{S_{MNP}}=\dfrac{6}{6\sqrt{3}}=\dfrac{1}{\sqrt{3}}\Rightarrow\alpha\approx54^044'\)


a, \(2sin^2x+\sqrt{3}sin2x=3\)
\(\Leftrightarrow-\left(1-2sin^2x\right)+\sqrt{3}sin2x=2\)
\(\Leftrightarrow\sqrt{3}sin2x-cos2x=2\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=1\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{6}\right)=1\)
\(\Leftrightarrow2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{3}+k\pi\)
d, \(cosx-\sqrt{3}sinx=2cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow-2sin\dfrac{\pi}{3}.sinx=0\)
\(\Leftrightarrow sinx=0\)
\(\Leftrightarrow x=k\pi\)


\(lim_{n\rightarrow+\infty}\dfrac{6^n+1}{6^n-2}=\)\(lim_{n\rightarrow+\infty}\dfrac{6^n\left(1+\dfrac{1}{6^n}\right)}{6^n\left(1-\dfrac{2}{6^n}\right)}=\)\(lim_{n\rightarrow+\infty}\dfrac{\left(1+\dfrac{1}{6^n}\right)}{\left(1-\dfrac{2}{6^n}\right)}=\dfrac{1}{1}=1\)
\(lim_{n\rightarrow-\infty}\dfrac{6^n+1}{6^n-2}=\)\(\dfrac{0+1}{0-2}=\dfrac{-1}{2}\)



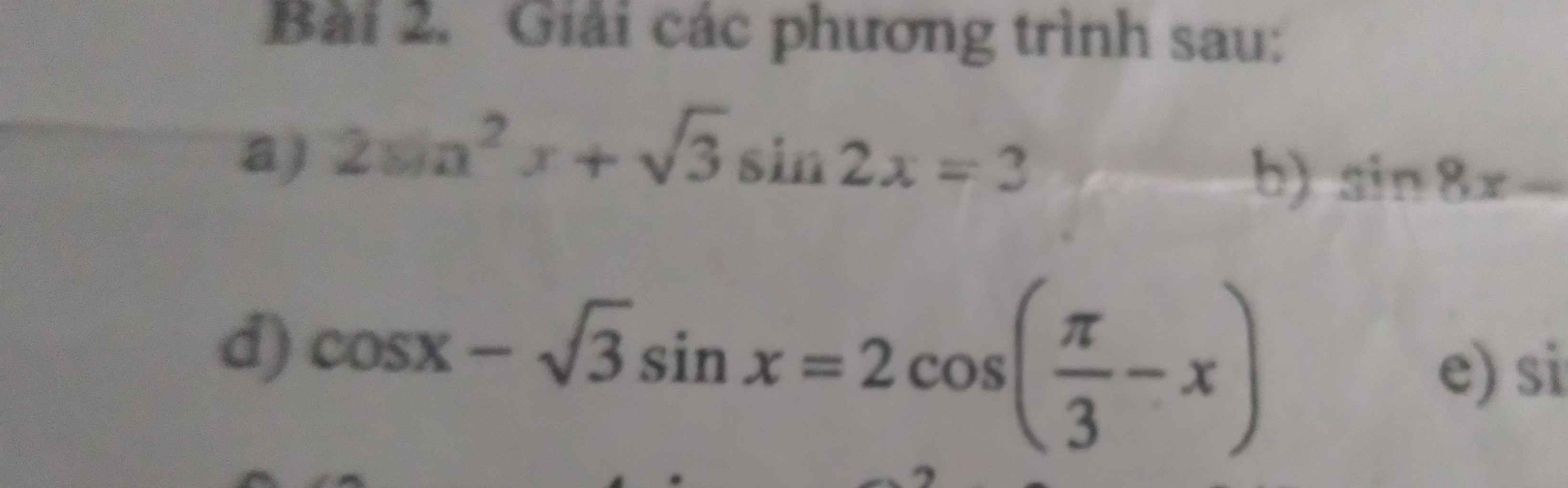






 ai giải giúp em với ạ
ai giải giúp em với ạ
1, \(\overrightarrow{v}=\overrightarrow{AB}=\left(1;3\right)\)
2, \(\overrightarrow{MM'}=\overrightarrow{v}=\left(2;3\right)\)
⇒ M' (3;6)
3, \(T_{\overrightarrow{v}}\left(d\right)=d'\) Ta có A(1 ; 0) ∈ d
⇒ \(\)d // d' và d đi qua A' = \(T_{\overrightarrow{v}}\left(A\right)\)
Tìm tọa độ A' rồi viết phương trình d' nhé