Ai giúp em câu này với ạ :((
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 11 2021
\(\Leftrightarrow sinx\left[m-1+2cosx\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cosx=\dfrac{1-m}{2}\end{matrix}\right.\)
\(sinx=0\Rightarrow x=k\pi\) có đúng 1 nghiệm \(x=\pi\) trên khoảng đã cho
\(\Rightarrow cosx=\dfrac{1-m}{2}\) có 2 nghiệm trên \(\left(0;2\pi\right)\)
\(\Rightarrow-1< \dfrac{1-m}{2}< 1\)
\(\Rightarrow-1< m< 3\Rightarrow m=\left\{0;1;2\right\}\) có 3 giá trị
12 tháng 7 2023
a: SA=SB=SC=SD
Đáy là hình vuông ABCD
=>S.ABCD là hình chóp đều
=>SO vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SC
2
18 tháng 12 2022
Có: `-C_2021 ^0 +C_2021 ^1 -C_2021 ^2 +....+C_2021 ^2019-C_2021 ^2020 -C_2021 ^2021 =-1-1=-2`
Mà `C_2021 ^0 +C_2021 ^1 +C_2021 ^2 +....+C_2021 ^2019 +C_2021 ^2020 +C_2021 ^2021 =2^2021`
`=>2(C_2021 ^1 + C_2021 ^3 +C_2021 ^5 +...+C_2021 ^2017 + C_2021 ^2019 )=-2+2^2021`
`=>C_2021 ^1 + C_2021 ^3 +...+C_2021 ^2017 + C_2021 ^2019 =-1+2^2020`
DN
1
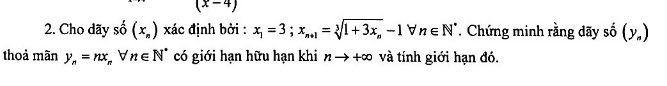
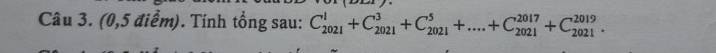
\(lim_{n\rightarrow+\infty}\dfrac{6^n+1}{6^n-2}=\)\(lim_{n\rightarrow+\infty}\dfrac{6^n\left(1+\dfrac{1}{6^n}\right)}{6^n\left(1-\dfrac{2}{6^n}\right)}=\)\(lim_{n\rightarrow+\infty}\dfrac{\left(1+\dfrac{1}{6^n}\right)}{\left(1-\dfrac{2}{6^n}\right)}=\dfrac{1}{1}=1\)
\(lim_{n\rightarrow-\infty}\dfrac{6^n+1}{6^n-2}=\)\(\dfrac{0+1}{0-2}=\dfrac{-1}{2}\)