Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(\begin{array}{l}f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}{x^2} - \frac{1}{2}}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {{x^2} - 1} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{1}{2}\left( {x + 1} \right) = \frac{1}{2}\left( {1 + 1} \right) = 1\end{array}\)
b) Phương trình đường thẳng \(d\) đi qua điểm \(M\left( {1;\frac{1}{2}} \right)\) và có hệ số góc bằng \(k = f'\left( 1 \right) = 1\) là: \(y - \frac{1}{2} = 1\left( {x - 1} \right) \Leftrightarrow y = x - 1 + \frac{1}{2} \Leftrightarrow y = x - \frac{1}{2}\).

Đường thẳng \(d\) cắt đồ thị hàm số \(\left( C \right)\) tại duy nhất điểm \(M\left( {1;\frac{1}{2}} \right)\).

b)
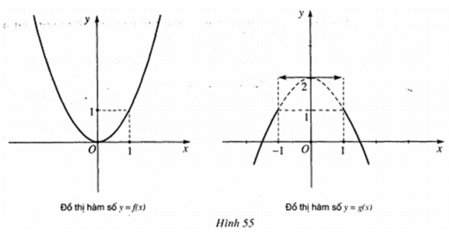
+ Đồ thị của hàm số y = f(x) là đường liền nét tại điểm có hoành độ x= 1.
+ Đồ thị hàm số y = g(x) là đường không liền nét tại điểm có hoành độ x= 1.

a) Đồ thị hàm số (hình bên).
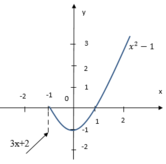
Quan sát đồ thị nhận thấy :
+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).
+ f(x) không liên tục tại x = -1.
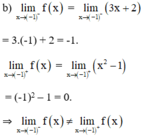
⇒ không tồn tại giới hạn của f(x) tại x = -1.
⇒ Hàm số không liên tục tại x = -1.

Ta có bảng sau:

Ta có đồ thị sau:
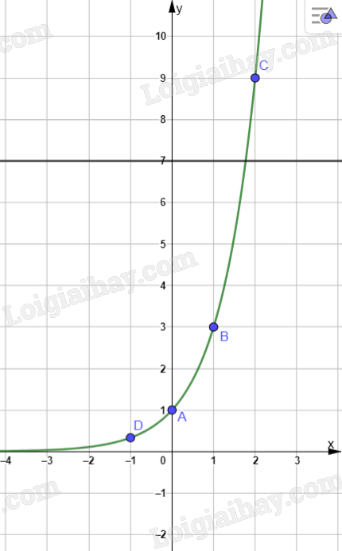
b, Hai đồ thị \(y=3^x\) và \(y=7\) có \(1\) giao điểm. Vậy số nghiệm của phương trình \(3^x=7\) là \(1\)

a:
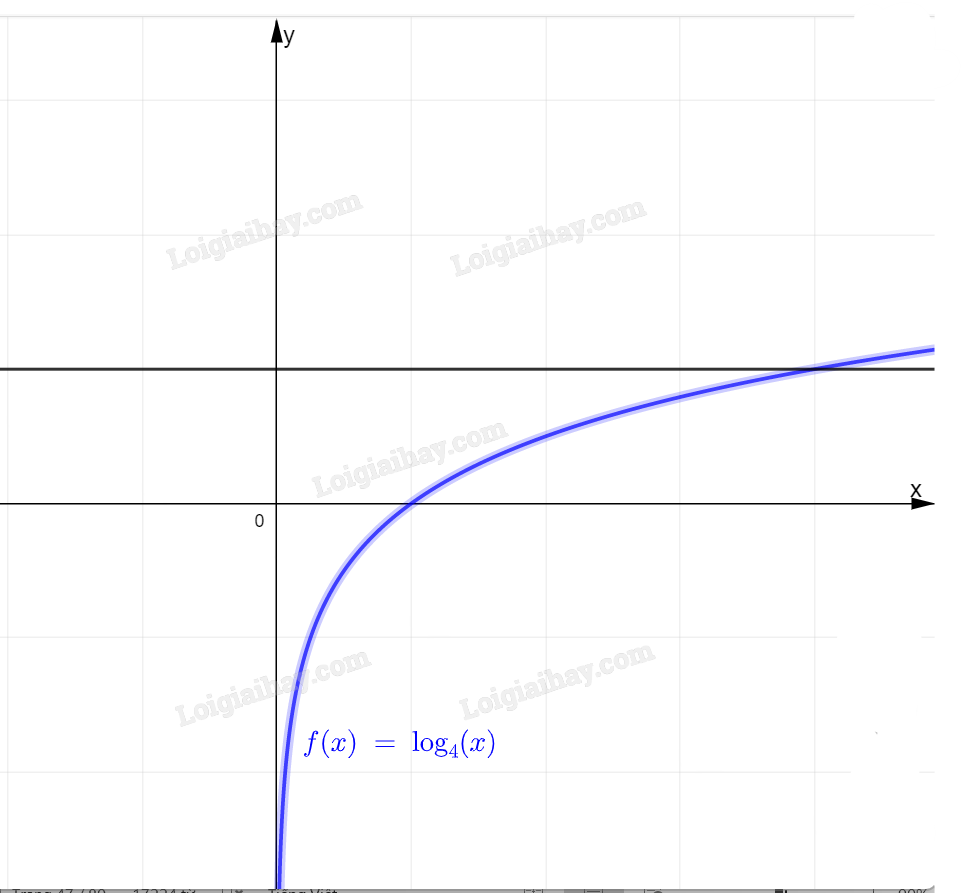
b: Hai đồ thị này có 1 giao điểm
=>Phương trình \(log_4x=5\) có 1 nghiệm duy nhất

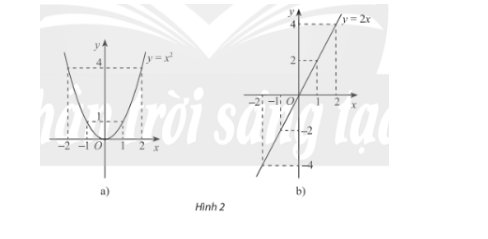
* Hàm số \(y = {x^2}\)
Nhìn đồ thị ta thấy:
+ \(y(1) = y( - 1) = 1,y(2) = y( - 2) = 4\)
+ Đồ thị hàm số đối xứng qua trục Oy.
* Hàm số \(y = 2x\)
Nhìn đồ thị ta thấy:
+ \(y(1) = - y( - 1),y(2) = - y( - 2)\)
+ Đồ thị hàm số đối xứng qua điểm O.

a) Các bạn tự vẽ hình nhé . Đồ thị hàm số y = f(x) là một đường không liền nét mà bị đứt quãng tại x0 = -1. Vậy hàm số đã cho liên tục trên khoảng (-∞; -1) và (- 1; +∞).
b) +) Nếu x < -1: f(x) = 3x + 2 liên tục trên (-∞; -1) (vì đây là hàm đa thức).
+) Nếu x> -1: f(x) = x2 – 1 liên tục trên (-1; +∞) (vì đây là hàm đa thức).
+) Tại x = -1;
Ta có =![]() = 3(-1) +2 = -1.
= 3(-1) +2 = -1.
![]() = (-1)2 – 1 = 0.
= (-1)2 – 1 = 0.
Vì ![]() nên không tồn tại
nên không tồn tại  . Vậy hàm số gián đoạn tại
. Vậy hàm số gián đoạn tại
x0 = -1.

a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{mx-1}{2x+m}=\lim\limits_{x\rightarrow+\infty}\dfrac{m-\dfrac{1}{x}}{2+\dfrac{m}{x}}=\dfrac{m}{2}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{mx-1}{2x+m}=\lim\limits_{x\rightarrow-\infty}\dfrac{m-\dfrac{1}{x}}{2+\dfrac{m}{x}}=\dfrac{m}{2}\)
Vậy: x=m/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{mx-1}{2x+m}\)
Để x=m/2 đi qua \(A\left(-1;\sqrt{2}\right)\) thì \(\dfrac{m}{2}=-1\)
=>\(m=-1\cdot2=-2\)
b: \(\lim\limits_{x\rightarrow-\infty}\dfrac{x-2}{2x-m}=\lim\limits_{x\rightarrow-\infty}\dfrac{1-\dfrac{2}{x}}{2-\dfrac{m}{x}}=\dfrac{1}{2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{x-2}{2x-m}=\lim\limits_{x\rightarrow+\infty}\dfrac{1-\dfrac{2}{x}}{2-\dfrac{m}{x}}=\dfrac{1}{2}\)
=>x=1/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{x-2}{2x-m}\)
=>Không có giá trị nào của m để đường thẳng x=1 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x-2}{2x-m}\)
- Giả sử Δx là số gia của đối số tại xo = 1. Ta có:
- Đường thẳng có hệ số góc bằng f'(1) = 1 có dạng:
y = 1.x + a hay y = x + a
Mà đường thẳng đó đi qua điểm M(1;1/2) nên có: 1/2 = 1 + a ⇒ a = 1/2 - 1 = -1/2
⇒ đường thẳng đi qua M và có hệ số góc bằng 1 là: y = x – 1/2
Ta có đồ thị như trên. Đường thẳng y = x – 1/2 tiếp xúc với đồ thị hàm số f(x) tại M