Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

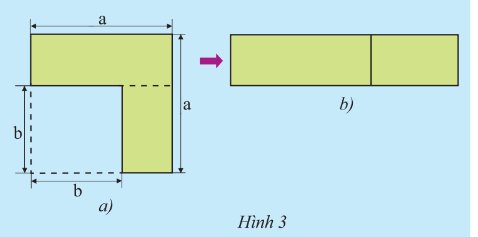
a) Diện tích Hình 3a là: \({a^2} - {b^2}\)
Diện tích Hình 3b là: \(\left( {a + b} \right)\left( {a - b} \right)\)
b) Ta có: \(\left( {a + b} \right)\left( {a - b} \right) = a.a - ab + ba - {b^2} = {a^2} - ab + ab - {b^2} = {a^2} - {b^2}\)
Suy ra: \(\left( {a + b} \right)\left( {a - b} \right) = {a^2} - {b^2}\)
Vậy diện tích của hai hình bằng nhau.

a) Trên đĩa cân bên trái ta thấy có 4 quả cân, mỗi quả có khối lượng \(x\) gam nên khối lượng đĩa cân bên trái là: \(x + x + x + x\) (gam)
Trên đĩa cân bên phải ta thấy có 2 quả cân, một quả có khối lượng \(x\) gam và một quả có khối lượng 600 gam nên khối lượng đĩa cân bên phải là: \(x + 600\) gam.
Từ điều kiện cân thăng bằng ta có biểu thức mối quan hệ sau:
\(x + x + x + x = x + 600\) hay \(4x = 600 + x\)
b) Nếu \(x = 200\) thì khối lượng đĩa cân bên trái là: \(4.200 = 800\) (gam); khối lượng đĩa cân bên phải là \(200 + 600 = 800\) (gam).
Do đó, cân thăng bằng.
Nếu \(x = 100\) thì khối lượng đĩa cân bên trái là: \(4.100 = 400\) (gam); khối lượng đĩa cân bên phải là \(100 + 600 = 700\) (gam).
Do đó, cân không thăng bằng.

a:
Diện tích xung quanh của hình hộp chữ nhật là:
\(\left(x+2y\right)\cdot3z=3xz+6yz\left(cm^2\right)\)
Diện tích 1 mặt là:
\(x\cdot2y=2xy\left(cm^2\right)\)
Tổng diện tích các mặt của hình hộp chữ nhật có 3 kích thước là x cm; 2y cm; 3z cm là:
\(3xz+6yz+2\cdot2xy=3xz+6yz+4xy\left(cm^2\right)\)
b: Thay x=6;y=2;z=3 vào 3xz+6yz+4xy, ta được:
\(3\cdot6\cdot3+6\cdot2\cdot3+4\cdot6\cdot2=54+36+48=138\left(cm^2\right)\)
a) Hình hộp chữ nhật có ba kích thước lần lượt là x (cm), 2y (cm), 3z (cm). Khi đó:
Diện tích xung quanh của hình hộp chữ nhật đó là:
(x + 2y).3z = 3xz + 6yz (cm2).
Diện tích hai đáy của hình hộp chữ nhật đó là:
2 . x . 2y = 4xy (cm2).
Tổng diện tích các mặt của hình hộp chữ nhật là:
4xy + 3xz + 6yz (cm2).
Vậy đa thức S biểu thị tổng diện tích các mặt của hình hộp chữ nhật đã cho là:
S = 4xy + 3xz + 6yz (cm2).
b) Giá trị của S tại x = 6; y = 2; z = 3 là:
4 . 6 . 2 + 3 . 6 . 3 + 6 . 2 . 3 = 48 + 54 + 36 = 138.