I
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 6 2023
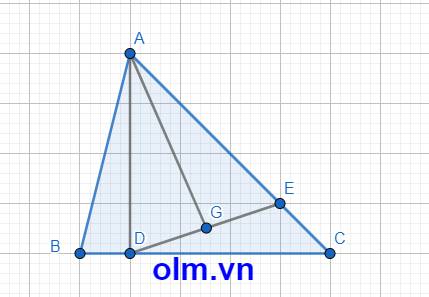
SADE = 2\(\times\)SAGE ( vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DE và DE = 2\(\times\) GE )
⇒ SADE = 36 \(\times\) 2 = 72 (cm2)
SADE = \(\dfrac{3}{4}\)\(\times\)SADC (vì hai tam giác có chung chiều cao hạ từ Đỉnh D xuống đáy AC và AE = \(\dfrac{3}{4}\)AC)
⇒ SACD = 72 : \(\dfrac{3}{4}\) = 96 (cm2)
DC = BC - BD = BC - \(\dfrac{1}{5}\)BC = \(\dfrac{4}{5}\)BC
SADC = \(\dfrac{4}{5}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và DC = \(\dfrac{4}{5}\)BC)
⇒ SABC = 96 : \(\dfrac{4}{5}\) = 120 (cm2)
Tỉ số phần trăm diện tích tam giác ADE và diện tích tam giác ABC là:
72 : 120 = 0,6
0,6 = 60%
Đáp số: 60%
4 tháng 4 2018
Hình như bn viết sai
Phải trên DA lấy trung điểm G(nếu như thế này thì mk lm đc )
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
27 tháng 10 2021
\(BD=BC\Rightarrow BD=BD=\frac{BC}{2}\)
Xét tg ABD và tg ABC có chung đường cao từ A->BC nên
\(\frac{S_{ABD}}{S_{ABC}}=\frac{BD}{BC}=\frac{1}{2}\Rightarrow S_{ABD}=\frac{S_{ABC}}{2}=\frac{30}{2}=15cm^2\)
Xét tg DEA; tg DEF và tg DBF có chung đường cao từ D->AB và AE=EF=FB nên
\(S_{DAE}=S_{DEF}=S_{DBF}\)
\(S_{ABD}=S_{DAE}+S_{DEF}+S_{DBF}=3xS_{DEF}=15\Rightarrow S_{DEF}=5cm^2\)
- Ta thấy :\(S_{AEG}=\frac{1}{4}S_{AEB}\)( vì có đáy EG = \(\frac{1}{4}\)đáy EB và có chung chiều cao là chiều cao hình thang . )
\(S_{AEB}=S_{AEG}\div\frac{1}{4}=20\div\frac{1}{4}=80\left(cm^2\right)\)
- Ta thấy :\(S_{AEB}=\frac{1}{3}S_{ABC}\) ( vì AE = EF = FC nên \(AE=\frac{1}{3}AC\)và có chung chiều cao là chiều cao hình thang )
\(\Rightarrow S_{ABC}=S_{AEB}\div\frac{1}{3}=80\div\frac{1}{3}=240\left(cm^2\right)\)
Đáp số : 240 cm2
Thử làm thôi , không biết đúng không ....
mk cũng ra 240 cm2 nhưng mk làm cách khác cơ !!!