Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Độ PH của mẫu 1 là:
\(a=-log\left[H^+\right]=-log\left[8\cdot10^{-7}\right]=-\left(log8-7\right)\)
\(=7-log8=7-log2^3=7-3\cdot log2\)
Độ PH của mẫu 2 là:
\(b=-log\left[2\cdot10^{-9}\right]=-\left(log2-9\right)=9-log2\)
\(a-b=7-3\cdot log2-9+log2=-2log2-2< 0\)
=>a<b
=>Độ PH của mẫu 2 lớn hơn

biến đổi về dạng 2 mũ 1/2 và 3 mũ 1/3 đi p.xong tách 3 mũ 1/3 thành 3^1/2 nhân 3^-1/6.so sánh 2^1/2 nhỏ hơn 3^1/2 do 2<3 nên 3^1/2 nhân 3^-1/6 sẽ lớn hơn 2^1/2.t giai v k pieets đúng k nua.sai thfi p thông cảm nhé

Đặt \(x+\dfrac{1}{x}=t\Rightarrow t^2=x^2+\dfrac{1}{x^2}+2\)
Pt trở thành:
\(7t+2\left(t^2-2\right)=5\Leftrightarrow2t^2+7t-9=0\)
\(\Rightarrow\left[{}\begin{matrix}t=1\\t=-\dfrac{9}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x+\dfrac{1}{x}=1\\x+\dfrac{1}{x}=-\dfrac{9}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-x+1=0\left(vô-nghiệm\right)\\x^2+\dfrac{9}{2}x+1=0\end{matrix}\right.\)
Theo hệ thức Viet: \(x_1x_2=\dfrac{c}{a}=1\)

Ta có: \(lim\dfrac{3-2x}{\sqrt{x}-3}=lim\dfrac{\dfrac{3}{x}-2}{\dfrac{1}{\sqrt{x}}-\dfrac{3}{x}}=-\infty\)
Vì: \(lim\left(\dfrac{3}{x}-2\right)=-2< 0\)
\(lim\left(\dfrac{1}{\sqrt{x}}-\dfrac{3}{x}\right)=0\) và \(\dfrac{1}{\sqrt{x}}-\dfrac{3}{x}>0\) khi x vô cùng lớn.

`1)(a^[1/4]-b^[1/4])(a^[1/4]+b^[1/4])(a^[1/2]+b^[1/2])`
`=[(a^[1/4])^2-(b^[1/4])^2](a^[1/2]+b^[1/2])`
`=(a^[1/2]-b^[1/2])(a^[1/2]+b^[1/2])`
`=a-b`
`2)(a^[1/3]-b^[2/3])(a^[2/3]+a^[1/3]b^[2/3]+b^[4/3])`
`=(a^[1/3]-b^[2/3])[(a^[1/3])^2+a^[1/3]b^[2/3]+(b^[2/3])^2]`
`=(a^[1/3])^3-(b^[2/3])^3`
`=a-b^2`

:)) không ai lại bấm máy tính cả , tất cả sẽ đơn giản khi giải bằng logarit.
\(333333,33333.10^5=\frac{x}{888888,888888.10^6}\left(x>0\right)\)\(\Leftrightarrow log_e\left(333333,33333.10^5\right)=log_e\left(\frac{x}{888888,888888\cdot10^6}\right)\)
\(\Leftrightarrow ln\left(\frac{33333333333}{100000}.10^5\right)=ln\left(\frac{x}{\frac{111111111111}{125000}\cdot10^6}\right)\)
\(\Leftrightarrow ln\left(\frac{33333333333}{100000}\cdot10^5\right)=ln\left(\frac{125000x}{111111111111.10^6}\right)\)
\(\Leftrightarrow ln\left(33333333333\right)-ln10^5+5ln10=ln\left(\frac{125000x}{111111111111.10^6}\right)\)
\(\Leftrightarrow ln\left(33333333333\right)=ln\left(125000x\right)-ln\left(111111111111.10^6\right)\)
\(\Leftrightarrow ln\left(33333333333.111111111111.10^6\right)=ln\left(125000\right)+ln\left(x\right)\)
\(\Leftrightarrow ln\left(\frac{33333333333.111111111111.10^6}{125000}\right)=lnx\)
\(\Rightarrow x=e^{\left(\frac{33333333333.111111111111.10^6}{125000}\right)}\)hoặc \(x=\frac{33333333333.111111111111.10^6}{125000}\)
à nhầm phải là \(x=e^{ln\left(\frac{33333333333.111111111111.10^6}{125000}\right)}\)

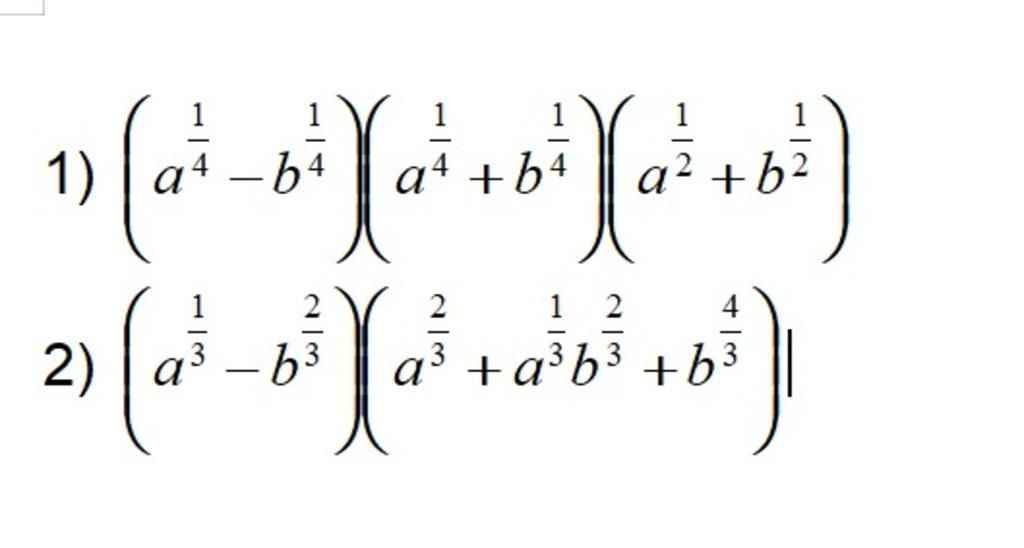
nghỉ nha
9999999999999999999999999999999999999999999999999999999999999999999999999999999999999999x1009999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999 = 9999999999999999999999999999999999999999999999999999999999999999999999999999999999999999x1009999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999