Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Độ PH của mẫu 1 là:
\(a=-log\left[H^+\right]=-log\left[8\cdot10^{-7}\right]=-\left(log8-7\right)\)
\(=7-log8=7-log2^3=7-3\cdot log2\)
Độ PH của mẫu 2 là:
\(b=-log\left[2\cdot10^{-9}\right]=-\left(log2-9\right)=9-log2\)
\(a-b=7-3\cdot log2-9+log2=-2log2-2< 0\)
=>a<b
=>Độ PH của mẫu 2 lớn hơn

mình ko ấn dấu lim, bn tự biết thêm vào nhé:
\(\frac{x^2-4x+3}{\sqrt{4x+5}-3}=\frac{\left(x-3\right)\left(x-1\right)\left(\sqrt{4x+5}+3\right)}{4x-4}=\frac{\left(x-3\right)\left(\sqrt{4x+5}+3\right)}{4}=-3\)

Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = 2x - x2 và y = -x là :

Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = 2x - x2 và y = -x là :
![]()
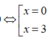
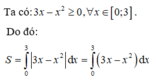
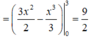

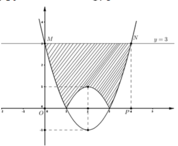
1.
Trước hết bạn nhớ công thức:
$1^2+2^2+....+n^2=\frac{n(n+1)(2n+1)}{6}$ (cách cm ở đây: https://hoc24.vn/cau-hoi/tinh-tongs-122232n2.83618073020)
Áp vào bài:
\(\lim\frac{1}{n^3}[1^2+2^2+....+(n-1)^2]=\lim \frac{1}{n^3}.\frac{(n-1)n(2n-1)}{6}=\lim \frac{n(n-1)(2n-1)}{6n^3}\)
\(=\lim \frac{(n-1)(2n-1)}{6n^2}=\lim (\frac{n-1}{n}.\frac{2n-1}{6n})=\lim (1-\frac{1}{n})(\frac{1}{3}-\frac{1}{6n})\)
\(=1.\frac{1}{3}=\frac{1}{3}\)
2.
\(\lim \frac{1}{n}\left[(x+\frac{a}{n})+(x+\frac{2a}{n})+...+(x.\frac{(n-1)a}{n}\right]\)
\(=\lim \frac{1}{n}\left[\underbrace{(x+x+...+x)}_{n-1}+\frac{a(1+2+...+n-1)}{n} \right]\)
\(=\lim \frac{1}{n}[(n-1)x+a(n-1)]=\lim \frac{n-1}{n}(x+a)=\lim (1-\frac{1}{n})(x+a)\)
\(=x+a\)


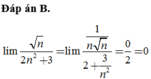
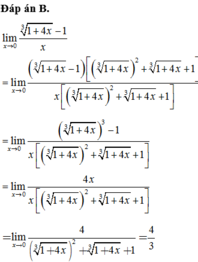
Ta có: \(lim\dfrac{3-2x}{\sqrt{x}-3}=lim\dfrac{\dfrac{3}{x}-2}{\dfrac{1}{\sqrt{x}}-\dfrac{3}{x}}=-\infty\)
Vì: \(lim\left(\dfrac{3}{x}-2\right)=-2< 0\)
\(lim\left(\dfrac{1}{\sqrt{x}}-\dfrac{3}{x}\right)=0\) và \(\dfrac{1}{\sqrt{x}}-\dfrac{3}{x}>0\) khi x vô cùng lớn.