K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
HP
13 tháng 12 2020
a. Trừ vế theo vế \(\left(1\right)\) cho \(\left(2\right)\) ta được \(x^2-y^2=4x-4y\)
\(\Leftrightarrow\left(x-y\right)\left(x+y-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=y\\x=4-y\end{matrix}\right.\)
TH1: \(x=y\)
Phương trình \(\left(1\right)\) tương đương:
\(x^2=2x\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=y=0\\x=y=2\end{matrix}\right.\)
TH2: \(x=4-y\)
Phương trình \(\left(2\right)\) tương đương:
\(y^2=4y-4\)
\(\Leftrightarrow y^2-4y+4=0\)
\(\Leftrightarrow\left(y-2\right)^2=0\)
\(\Leftrightarrow y=2\)
\(\Rightarrow x=2\)
Vậy hệ đã cho có nghiệm \(\left(x;y\right)\in\left\{\left(0;0\right);\left(2;2\right)\right\}\)
b. \(\left\{{}\begin{matrix}x+y+xy=5\\x^2+y^2=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=5-\left(x+y\right)\\\left(x+y\right)^2-2xy=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=5-\left(x+y\right)\\\left(x+y\right)^2-10+2\left(x+y\right)=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=5-\left(x+y\right)\\\left(x+y\right)^2+2\left(x+y\right)-15=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=5-\left(x+y\right)\\\left(x+y+5\right)\left(x+y-3\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=5-\left(x+y\right)\\\left[{}\begin{matrix}x+y=-5\\x+y=3\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+y=-5\\xy=10\end{matrix}\right.\\\left\{{}\begin{matrix}x+y=3\\xy=2\end{matrix}\right.\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}x+y=-5\\xy=10\end{matrix}\right.\Leftrightarrow\) vô nghiệm
TH2: \(\left\{{}\begin{matrix}x+y=3\\xy=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\\\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\end{matrix}\right.\)
Vậy ...
CM
27 tháng 10 2018
Ta có: x 2 + x y + y 2 = 4 x + y + x y = 2 ⇔ x + y 2 - x y = 4 x + y + x y = 2
Đặt S= x+ y; P = xy. Khi đó hệ phương trình trên trở thành: S 2 - P = 4 ( 1 ) S + P = 2 ( 2 )
Từ (2) suy ra: P= 2- S thay (1): S2 - (2 – S) = 4
⇔ S 2 + S - 6 = 0 ⇔ [ S = - 3 S = 2
* Với S = -3 thì P = 5. Khi đó,x, y là nghiệm phương trình: t2 + 3t + 5 = 0 ( vô nghiệm).
* Với S= 2 thì P = 0. Khi đó, x, y là nghiệm phương trình:
t2 – 2t = 0 ⇔ [ t = 0 t = 2
Do đó, có 2 cặp số thỏa mãn là ( 0; 2) và(2; 0).
Chọn B.
CM
13 tháng 4 2019
Phương trình 1 ⇔ x + y 2 x - y = 0 ⇔ x = − y 2 x = y
Trường hợp 1: x = - y thay vào (2) ta được x 2 - 4 x + 3 = 0 ⇔ x = 1 x = 3
Suy ra hệ phương trình có hai nghiệm là (1; −1), (3; −3).
Trường hợp 2: 2 x = y thay vào (2) ta được - 5 x 2 + 17 x + 3 = 0 phương trình này không có nghiệm nguyên.
Vậy các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là (1; −1) và (3; −3).
Đáp án cần chọn là: C
PH
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
Phương trình đã cho là đường tròn khi:
\(m^2+4\left(m-2\right)^2-6>0\)
\(\Leftrightarrow5m^2-16m+10>0\)
\(\Rightarrow\left[{}\begin{matrix}m>\dfrac{8+\sqrt{14}}{5}\\m< \dfrac{8-\sqrt{14}}{5}\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
19 tháng 5 2020
Lời giải:
Tiếp tuyến $(d')$ cần tìm song song với $(d): x+y-3=0$ nên có dạng $x+y+m=0$
Viết lại PTĐTr $(C): (x-1)^2+(y+2)^2=8$
$\Rightarrow$ tâm $I(1;-2)$ và bán kính $R=2\sqrt{2}$
Vì $(d')$ là tiếp tuyến của $(C)$ nên: \(d(I, d')=R\Leftrightarrow \frac{|x_I+y_I+m|}{\sqrt{1^2+1^2}}=2\sqrt{2}\)
\(\Leftrightarrow |m-1|=4\Rightarrow m=5\) hoặc $m=-3$. TH $m=-3$ loại do trùng với $(d)$
Vậy PTTT cần tìm là $x+y+5=0$
TT
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2022
Đường tròn (C) có tâm \(I\left(\dfrac{3}{2};-2\right)\Rightarrow\overrightarrow{IM}=\left(-\dfrac{5}{2};5\right)=-\dfrac{5}{2}\left(1;-2\right)\)
Đường thẳng d tiếp xúc (C) tại M nên \(IM\perp d\Rightarrow d\) nhận (1;-2) là 1 vtpt
Phương trình tiếp tuyến d:
\(1\left(x+1\right)-2\left(y-3\right)=0\Leftrightarrow x-2y+7=0\)
KN
31 tháng 1 2020
Bạn tham khảo nhé!
Câu hỏi của Lê VĂn Chượng - Toán lớp 10 - Học toán với OnlineMath
L
23 tháng 1 2022
(C1) tâm I1(0;2) và R1= 3;
(C2) tâm I2( 3;-4) và R2= 3
- Nhận xét :
không cắt C2
- Gọi d: ax+ by+ c= 0 là tiếp tuyến chung , thế thì : d(I1; d) = R1 và d (I2; d) = R2
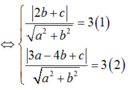
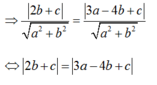
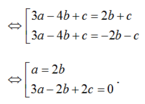
- Trường hợp: a= 2b thay vào (1):
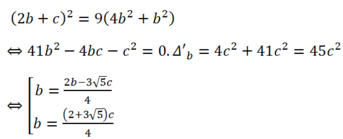
- Do đó ta có hai đường thẳng cần tìm :
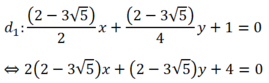
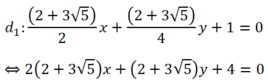
- Trường hợp :
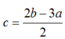
thay vào :
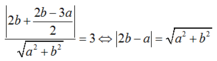
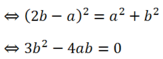
-Có 2 đường thẳng : d3: 2x- 1 = 0 và d4: 6x + 8y -1= 0.
Có tất cả 4 tiếp tuyến chung.
pt(1)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=0\\3x^2+\left(6+y^2\right)x+2y^2=0\left(1'\right)\end{array}\right.\)
*)x=0.Thay vào pt(2) ta đc:y\(^2\)=-3(VN)
*)(1')\(\Leftrightarrow\left(x+2\right)\left(y^2+3x\right)=0\Leftrightarrow\left[\begin{array}{nghiempt}x=-2\\y^2=-3x\end{array}\right.\)
TH1:x=-2\(\Rightarrow y^2\)=-5(VN)
TH2:y\(^2\)=-3x.(x\(\le0\)).Thay vào pt(2) ta đc:\(^2\)x\(^2\)
\(\Rightarrow\)x=3(L) hoặc x=1(L)
Vậy hệ pt vô nghiệm