Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A.
Dựa vào bảng đã cho ta có bảng phân bố tần số; tần suất như sau:
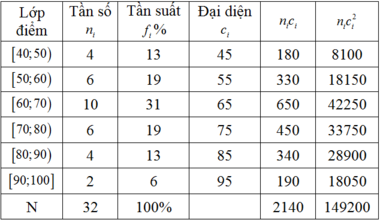
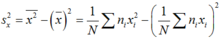
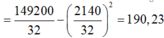
ập xác định D = R.
Giải từng bất phương trình ta có:
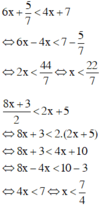
Vậy tập nghiệm của hệ bất phương trình là
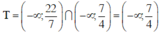
Ta lập bảng phân bố tần số ghép lớp:
Lớp |
L 1 |
L 2 |
L 3 |
L 4 |
L 5 |
L 6 |
|
Tần số |
4 |
6 |
11 |
6 |
3 |
2 |
n=32 |
Số học sinh có số điểm trong nửa khoảng [50,80) là 6+11+6=23
Chọn A
a) Đồng bằng sông Hồng:
23 27 34 35 37 39 46 54 57 57 187
n=11.
Số trung bình: \(\overline X \approx 54,18\)
Trung vị: 39
Tứ phân vị: \({Q_1} = 34,{Q_3} = 57\)
Mốt là 57 vì có tần số là 2 (xuất hiện 2 lần).
Khoảng biến thiên: R=187-23=164
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 57 - 34 = 23\)
Ta có bảng sau:
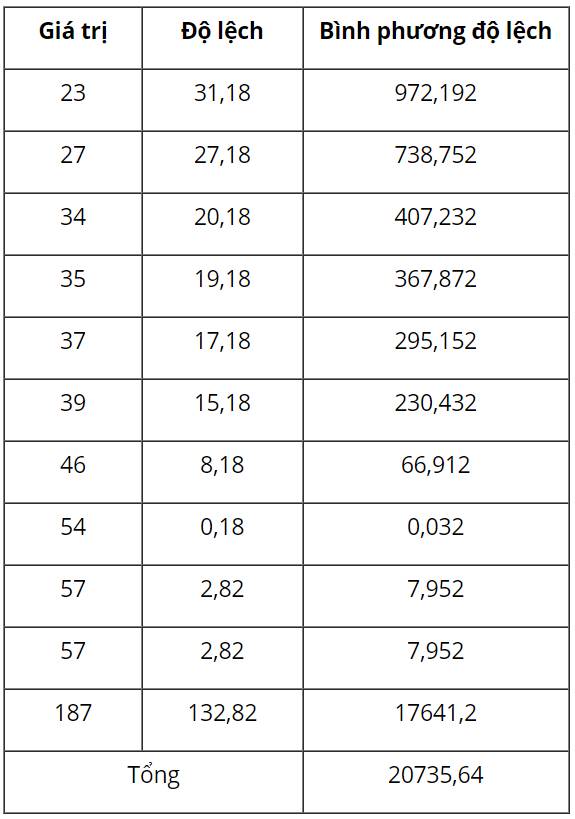
Độ lệch chuẩn: 144
Đồng bằng sông Cửu Long:
15 19 23 24 24 24 26 29 33 33 34 39 42
n=13
Số trung bình: \(\overline X \approx 28,1\)
Trung vị: 26
Tứ phân vị: \({Q_1} = 23,5,{Q_3} = 33,5\)
Mốt là 24 vì có tần số là 3 (xuất hiện 3 lần).
Khoảng biến thiên: R=42-15=27
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 33,5 - 23,5 = 10\)
Ta có bảng sau:
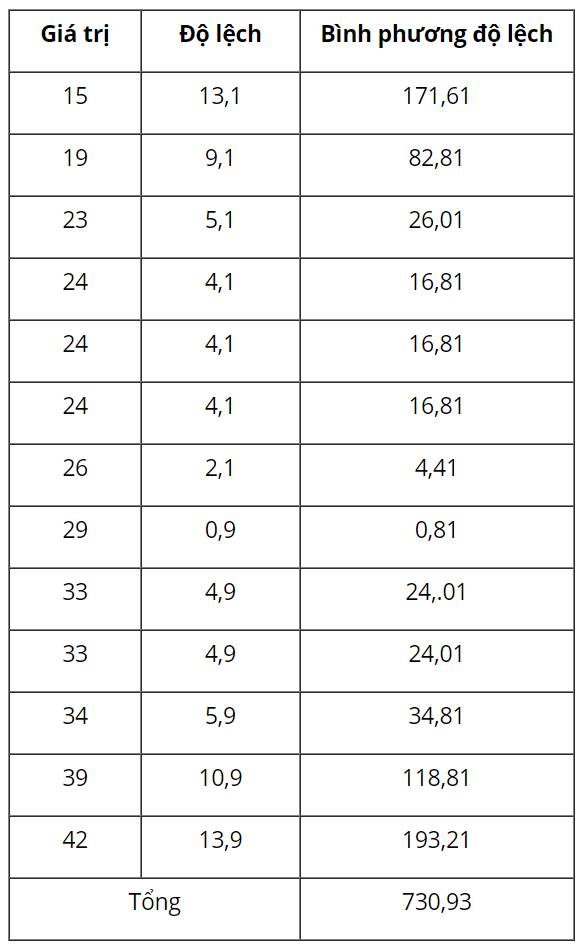
Độ lệch chuẩn: 27,04
b) Số trung bình sai khác vì ở Đồng bằng sông Hồng thì có giá trị bất thường là 187 (cao hơn hẳn giá trị trung bình), còn ở Đồng bằng sông Cửu Long thì không có giá trị bất thường.
Chính giá trị bất thường làm nên sự sai khác đó, còn trung vị không bị ảnh hưởng đến giá trị bất thường nên trung vị ở hai mẫu đều như nhau.
c) Giá trị bất thường ảnh hưởng đến khoảng biến thiên và độ lệch chuẩn, còn với khoảng tứ phân vị thì không (khoảng tứ phân vị đo 50% giá trị ở chính giữa).
a)
+) Số trung bình: \(\overline x = \frac{{23.6 + 25.8 + 28.10 + 31.6 + 33.4 + 37.3}}{{6 + 8 + 10 + 6 + 4 + 3}} \approx 28,3\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm,
\(\underbrace {23,...,23}_6,\underbrace {25,...25}_8,\underbrace {28,...,28}_{10},\underbrace {31,...,31}_6,\underbrace {33,...,33}_4,37,37,37\)
Bước 2: \(n = 6 + 8 + 10 + 6 + 4 + 3 = 37\), là số lẻ \( \Rightarrow {Q_2} = {X_{19}} = 28\)
\({Q_1}\) là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\): \(\underbrace {23,...,23}_6,\underbrace {25,...25}_8,\underbrace {28,...,28}_4\)
Do đó \({Q_1} = \frac{1}{2}({X_9} + {X_{10}}) = \frac{1}{2}(25 + 25) = 25\)
\({Q_3}\) là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\)
\(\underbrace {28,...,28}_5,\underbrace {31,...,31}_6,\underbrace {33,...,33}_4,37,37,37\)
Do đó \({Q_3} = \frac{1}{2}({X_9} + {X_{10}}) = \frac{1}{2}(31 + 31) = 31\)
+) Mốt \({M_o} = 28\)
b) Giả sử cỡ mẫu \(n = 10\)
Khi đó ta có bảng số liệu như sau:
Giá trị | 0 | 2 | 4 | 5 |
Tần số | 6 | 2 | 1 | 1 |
+) Số trung bình: \(\overline x = \frac{{0.0,6 + 2.0,2 + 4.0,1 + 5.0,1}}{{0,6 + 0,2 + 0,1 + 0,1}} = 1,3\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm \(0,0,0,0,0,0,2,2,4,5\)
Bước 2: \(n = 10\), là số chẵn \( \Rightarrow {Q_2} = \frac{1}{2}(0 + 0) = 0\)
\({Q_1}\) là trung vị của nửa số liệu: \(0,0,0,0,0\). Do đó \({Q_1} = 0\)
\({Q_3}\) là trung vị của nửa số liệu: \(0,2,2,4,5\). Do đó \({Q_3} = 2\)
+) Mốt \({M_o} = 0\)
Cách 1:
+ Giá trị đại diện mỗi lớp: c 1 = 18 ; c 2 = 22 ; c 3 = 26 ; c 4 = 30 ; c 5 = 34
+ Số trung bình cộng:
x = n 1 c 1 + n 2 c 2 + n 3 c 3 + n 4 c 4 + n 5 c 5 n 1 + n 2 + n 3 + n 4 + n 5 = 10 . 18 + 12 . 22 + 14 . 26 + 9 . 30 + 5 . 34 50 ≈ 25
+ Độ lệch chuẩn:
s = s 2 = 10 18 - 25 2 + 12 22 - 25 2 + 14 26 - 25 2 + 9 30 - 25 2 + 5 34 - 25 2 50
≈ 5 , 0
Cách 2: Sử dụng máy tính Casio fx - 570 VNPLUS
+ Nhập 
(vào chế thống kê).
+ Nhập 
(hiển thị cột tần số).
+ Nhập 
(nhập giá trị).
+ Nhập 
(nhập tần số), sau đó ấn 
.
+ Nhập 
⇒ δ x = 4 , 983813801
(Lưu ý: Đối với Ví dụ 2, phương sai s 2 = 24 , 9 ).
Đáp án C.