Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) +) Mẫu số liệu đồng bằng sông Hồng:
Số trung bình của mẫu số liệu:
Sắp xếp số liệu trên theo thứ tự không giảm ta được:
23; 27; 34; 35; 37; 39; 46; 54; 57; 57; 187.
Vì n = 11 là số lẻ nên trung bị Q2 = 39.
Nửa số liệu bên trái có tứ phân vị thứ nhất là: Q1 = 34.
Nửa số liệu bên phải có tứ phân vị thứ ba là: Q3 = 57.
Khoảng tứ phân vị là:
ΔQ = Q3 – Q1 = 57 – 34 = 23.
Ta có giá trị lớn nhất của số liệu là 187 và giá trị nhỏ nhất là 23. Khi đó khoảng biến thiên là: R = 187 – 23 = 164.
Theo quan sát số liệu, ta thấy giá trị 57 có tần số suất hiện nhiều nhất nên mốt là 57.
+) Mẫu số liệu đồng bằng sông Cửu Long:
Số trung bình của mẫu số liệu:
Sắp xếp số liệu trên theo thứ tự không giảm ta được:
15; 19; 23; 24; 24; 24; 26; 29; 33; 33; 34; 39; 42.
Vì n = 13 là số lẻ nên trung vị Q2 = 26.
Nửa số liệu bên trái có tứ phân vị thứ nhất là: Q1 = (23 + 24):2 = 23,5.
Nửa số liệu bên phải có tứ phân vị thứ ba là: Q3 = (33 + 34):2 = 33,5.
Khoảng tứ phân vị là:
ΔQ = Q3 – Q1 = 33,5 – 23,5 = 10.
Ta có giá trị lớn nhất của số liệu là 42 và giá trị nhỏ nhất là 15. Khi đó khoảng biến thiên là: R = 42 – 15 = 27.
Theo quan sát số liệu, ta thấy giá trị 24 có tần số suất hiện nhiều nhất nên mốt là 24.
b) Vì trong mẫu số liệu thứ nhất có giá trị bất thường là 187, giá trị này làm ảnh hưởng đến giá trị trung bình của mẫu số liệu một nên có sự sai khác nhiều hai số trung bình của hai mẫu số liệu còn trung vị thì không.
c) Vì trong mẫu số liệu thứ nhất có giá trị bất thường là 187, giá trị này là giá trị lớn nhất nên ảnh hưởng đến khoảng biến thiên của mẫu số liệu một. Trong khi đó, các giá trị của mẫu số liệu hai không có giá trị nào bất thường. Do đó khoảng biến thiên của hai mẫu số liệu có sự chênh lệch nhau.
Độ phân tán của mẫu số liệu một lớn hơn nhiều so với độ phân tán của mẫu số liệu hai. Do đó độ lệch chuẩn của hai số liệu sau có sự khác biệt.
Khoảng tứ phân vị là khoảng biến thiên của 50% số liệu chính giữa mà các giá trị chính giữa của hai mẫu số liệu không quá chênh lệch. Do đó khoảng tứ phân vị của hai mẫu số liệu không quá khác biệt.

a) +) Mẫu số liệu đồng bằng sông Hồng:
Số trung bình của mẫu số liệu:
Sắp xếp số liệu trên theo thứ tự không giảm ta được:
23; 27; 34; 35; 37; 39; 46; 54; 57; 57; 187.
Vì n = 11 là số lẻ nên trung bị Q2 = 39.
Nửa số liệu bên trái có tứ phân vị thứ nhất là: Q1 = 34.
Nửa số liệu bên phải có tứ phân vị thứ ba là: Q3 = 57.
Khoảng tứ phân vị là:
ΔQ = Q3 – Q1 = 57 – 34 = 23.
Ta có giá trị lớn nhất của số liệu là 187 và giá trị nhỏ nhất là 23. Khi đó khoảng biến thiên là: R = 187 – 23 = 164.
Theo quan sát số liệu, ta thấy giá trị 57 có tần số suất hiện nhiều nhất nên mốt là 57.
+) Mẫu số liệu đồng bằng sông Cửu Long:
Số trung bình của mẫu số liệu:
Sắp xếp số liệu trên theo thứ tự không giảm ta được:
15; 19; 23; 24; 24; 24; 26; 29; 33; 33; 34; 39; 42.
Vì n = 13 là số lẻ nên trung vị Q2 = 26.
Nửa số liệu bên trái có tứ phân vị thứ nhất là: Q1 = (23 + 24):2 = 23,5.
Nửa số liệu bên phải có tứ phân vị thứ ba là: Q3 = (33 + 34):2 = 33,5.
Khoảng tứ phân vị là:
ΔQ = Q3 – Q1 = 33,5 – 23,5 = 10.
Ta có giá trị lớn nhất của số liệu là 42 và giá trị nhỏ nhất là 15. Khi đó khoảng biến thiên là: R = 42 – 15 = 27.
Theo quan sát số liệu, ta thấy giá trị 24 có tần số suất hiện nhiều nhất nên mốt là 24
b) Vì trong mẫu số liệu thứ nhất có giá trị bất thường là 187, giá trị này làm ảnh hưởng đến giá trị trung bình của mẫu số liệu một nên có sự sai khác nhiều hai số trung bình của hai mẫu số liệu còn trung vị thì không.
c) Vì trong mẫu số liệu thứ nhất có giá trị bất thường là 187, giá trị này là giá trị lớn nhất nên ảnh hưởng đến khoảng biến thiên của mẫu số liệu một. Trong khi đó, các giá trị của mẫu số liệu hai không có giá trị nào bất thường. Do đó khoảng biến thiên của hai mẫu số liệu có sự chênh lệch nhau.
Độ phân tán của mẫu số liệu một lớn hơn nhiều so với độ phân tán của mẫu số liệu hai. Do đó độ lệch chuẩn của hai số liệu sau có sự khác biệt.
Khoảng tứ phân vị là khoảng biến thiên của 50% số liệu chính giữa mà các giá trị chính giữa của hai mẫu số liệu không quá chênh lệch. Do đó khoảng tứ phân vị của hai mẫu số liệu không quá khác biệt.

Ví dụ, ta có bảng đo chiều cao của các bạn trong tổ như sau:
160 | 162 | 164 | 165 | 172 | 174 | 177 | 178 | 180 |
a) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
160 162 164 165 172 174 177 178 180
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{160\;\; + 162\;\; + 164\;\;\; + \;\;165\;\; + \;172\;\; + \;174\;\; + \;177\; + \;\;178\; + \;180}}{9} = \frac{{1532}}{9}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 9 số liệu ( lẻ ) nên trung vị \({Q_2} = 172\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 160 162 164 165 là: \({Q_1} = 163\)
- Trung vị của dãy 174 177 178 180 là: \({Q_3} = 177,5\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 163\), \({Q_2} = 172\), \({Q_3} = 177,5\)
b) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 180 - 160 = 20\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 177,5 - 163 = 14,5\)
c) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {160 - \overline x } \right)}^2} + {{\left( {162 - \overline x } \right)}^2} + ... + {{\left( {180 - \overline x } \right)}^2}} \right]}}{9} \approx 50,84\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 7,13\)

• Ta có:
- Số trung bình cộng x = 55,82 trường là không có nghĩa.
- Trong các số liệu thống kê đã cho có sự chênh lệch quá lớn (điều này chứng tỏ các số liệu thống kê đã cho là không cùng loại)
Chỉ cần một trong hai điều kể trên là đủ để suy ra rằng: Không chọn được số trung bình cộng làm đại diện cho các số liệu thống kê.
• Dễ thấy: Bảng số liệu thống kê đã cho không có mốt.
• Trong trường hợp đã cho, ta chọn số trung vị M e = 40 (trường) để làm đại diện cho các số liệu thống kê đã cho (về quy mô và độ lớn).
Đáp án: B

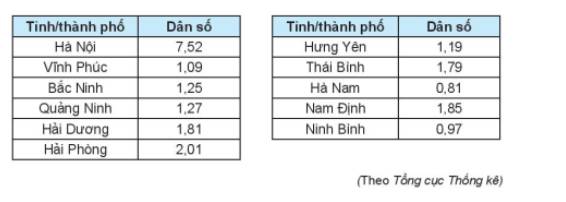
a)
Sắp xếp lại:
0,81 | 0,97 | 1,09 | 1,19 | 1,25 | 1,27 | 1,79 | 1,81 | 1,85 | 2,01 | 7,52 |
Số trung bình Có 11 tỉnh thành nên n=11.
\(\begin{array}{l}\overline X = \frac{{7,52 + ... + 1,19 + ... + 0,97}}{{11}}\\ = 1,96\end{array}\)
Trung vị: 1,27
b) Ta thấy 7,52 lệch hẳn so với giá trị trung bình nên đây là giá trị bất thường của mẫu số liệu
=> Số trung bình và trung vị lại có sự sai khác nhiều
c) Nên sử dụng trung vị để đại diện cho dân số của các tỉnh thuộc Đồng bằng Bắc Bộ.

Tham khảo:
n=10
Giả sử sau khi sắp xếp 10 số dương theo thứ tự không giảm thì được:

=> Trung vị là giá trị trung bình của số thứ 5 và thứ 6.
=> \({Q_1}\) là số thứ 3 và \({Q_3}\) là số thứ 8.
a) Khi nhân mỗi giá trị của mẫu số liệu với 2 thì:
+ Số lớn nhất tăng 2 lần và số nhỏ nhất tăng 2 lần
=> R tăng 2 lần
+ \({Q_1}\) và \({Q_3}\) tăng 2 lần
=> Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\) tăng 2 lần.
+ Giá trị trung bình tăng 2 lần
=> Độ lệch của mỗi giá trị so với giá trị trung bình \(\left| {{x_i} - \overline x} \right|\) cũng tăng 2 lần
=> \({\left( {{x_i} - \overline x} \right)^2}\) tăng 4 lần
=> Phương sai tăng 4 lần
=> Độ lệch chuẩn tăng 2 lần.
Vậy R tăng 2 lần, khoảng tứ phân vị tăng 2 lần và độ lệch chuẩn tăng 2 lần.
b) Cộng mỗi giá trị của mẫu số liệu với 2 thì
+ Số lớn nhất tăng 2 đơn vị và số nhỏ nhất tăng 2 đơn vị
=> R không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
+ \({Q_1}\) và \({Q_3}\) tăng 2 đơn vị
=> Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\) không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
+ Giá trị trung bình tăng 2 đơn vị
=> Độ lệch của mỗi giá trị so với giá trị trung bình \(\left| {{x_i} - \overline x} \right|\) không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
=> \({\left( {{x_i} - \overline x} \right)^2}\) không đổi
=> Phương sai không đổi.
=> Độ lệch chuẩn không đổi.
Vậy khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn đều không đổi.

Sắp xếp theo thứ tự không giảm.
2,593 2,977 3,155 3,270 3,387 3,412 3,813 3,920 4,042 4,236
Khoảng biến thiên \(R = 4,236 - 2,593 = 1,643\)
Vì n=10 nên ta có:
\({Q_1} = 3,155\); \({Q_3} = 3,920\)
Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1} = 3,920 - 3,155\)\( = 0,765\)
\(\overline x \approx 3,481\)
Ta có:
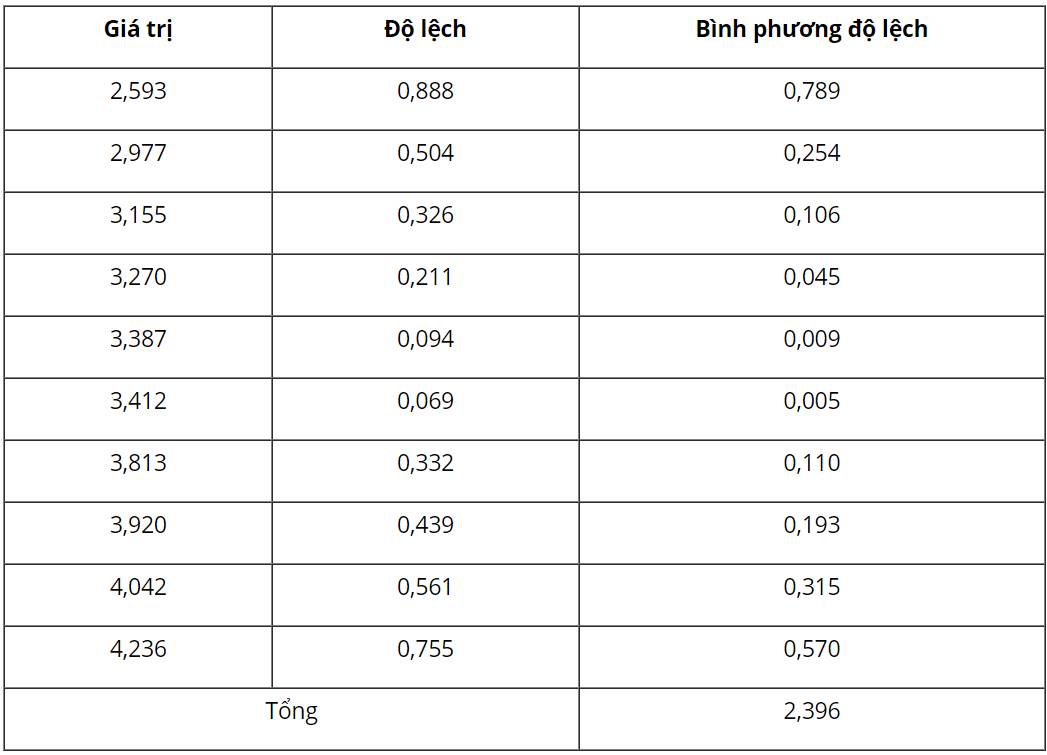
Độ lệch chuẩn: \(s = \sqrt {0,2396} \approx 0,489\)Phương sai là: \({s_2} = \frac{{2,396}}{{10}} = 0,2396\)

a. Số trung bình của đồng bằng sông Hồng là:
Đồng bằng sông Hồng:
(187 + 34 + 35 + 46 + 54 + 57 + 37 + 39 + 23 + 57 + 27):11\(\simeq\) 54,18
Vì n = 11 là số lẻ nên trung vị Q2 = 39.
Nửa số liệu bên trái có 5 giá trị nên tứ phân vị thứ nhất là: Q1 = 34.
Nửa số liệu bên phải có 5 giá trị nên tứ phân vị thứ ba là: Q3 = 57.
Khoảng tứ phân vị là:
ΔQ = Q3 – Q1 = 57 – 34 = 23.
Ta có giá trị lớn nhất của số liệu là 187 và giá trị nhỏ nhất là 23. Khi đó khoảng biến thiên là: R = 187 – 23 = 164.
Theo quan sát số liệu, ta thấy giá trị 57 có tần số xuất hiện nhiều nhất nên mốt là 57.
Ta có bảng sau:
|
Giá trị |
Độ lệch |
Bình phương độ lệch |
|
23 |
31,18 |
972,192 |
|
27 |
27,18 |
738,752 |
|
34 |
20,18 |
407,232 |
|
35 |
19,18 |
367,872 |
|
37 |
17,18 |
295,152 |
|
39 |
15,18 |
230,432 |
|
46 |
8,18 |
66,912 |
|
54 |
0,18 |
0,032 |
|
57 |
2,82 |
7,952 |
|
57 |
2,82 |
7,952 |
|
187 |
132,82 |
17 641,2 |
|
Tổng |
20 735,68 |
|
Phương sai:
Độ lệch chuẩn: .
Đồng bằng sông Cửu Long: (33+ 34 +33 + 29 + 24 + 39 + 42 + 24 + 23+ 19 + 24 + 15 + 26):13\(\simeq\)28,08
Vì n' = 13 là số lẻ nên trung vị Q'2 = 26.
Nửa số liệu bên trái có 6 giá trị nên tứ phân vị thứ nhất là: Q1 = (23 + 24):2 = 23,5.
Nửa số liệu bên phải có 6 giá trị nên tứ phân vị thứ ba là: Q3 = (33 + 34):2 = 33,5.
Khoảng tứ phân vị là:
Δ'Q = Q'3 – Q'1 = 33,5 – 23,5 = 10.
Ta có giá trị lớn nhất của số liệu là 42 và giá trị nhỏ nhất là 15. Khi đó khoảng biến thiên là: R' = 42 – 15 = 27.
Theo quan sát số liệu, ta thấy giá trị 24 có tần số xuất hiện nhiều nhất nên mốt là 24.
Ta có bảng sau:
|
Giá trị |
Độ lệch |
Bình phương độ lệch |
|
15 |
13,1 |
171,61 |
|
19 |
9,1 |
82,81 |
|
23 |
5,1 |
26,01 |
|
24 |
4,1 |
16,81 |
|
24 |
4,1 |
16,81 |
|
24 |
4,1 |
16,81 |
|
26 |
2,1 |
4,41 |
|
29 |
0,9 |
0,81 |
|
33 |
4,9 |
24,.01 |
|
33 |
4,9 |
24,01 |
|
34 |
5,9 |
34,81 |
|
39 |
10,9 |
118,81 |
|
42 |
13,9 |
193,21 |
|
Tổng |
730,93 |
|
Phương sai: .
Độ lệch chuẩn: .
b) Số trung bình sai khác vì ở Đồng bằng sông Hồng thì có giá trị bất thường là 187 (cao hơn hẳn so với các giá trị còn lại), còn ở Đồng bằng sông Cửu Long thì không có giá trị bất thường.
Chính giá trị bất thường làm nên sự sai khác đó, còn trung vị không bị ảnh hưởng đến giá trị bất thường nên trung vị ở hai mẫu số liệu không khác nhau quá nhiều.
c) Giá trị bất thường ảnh hưởng đến khoảng biến thiên và độ lệch chuẩn, còn với khoảng tứ phân vị thì không (khoảng tứ phân vị đo 50% giá trị ở chính giữa).
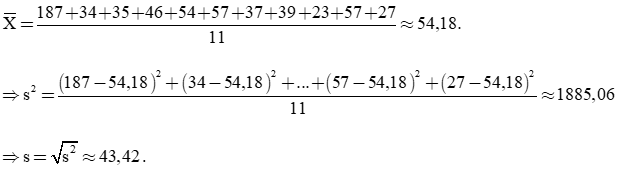
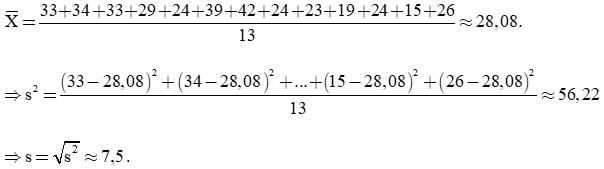

a) Đồng bằng sông Hồng:
23 27 34 35 37 39 46 54 57 57 187
n=11.
Số trung bình: \(\overline X \approx 54,18\)
Trung vị: 39
Tứ phân vị: \({Q_1} = 34,{Q_3} = 57\)
Mốt là 57 vì có tần số là 2 (xuất hiện 2 lần).
Khoảng biến thiên: R=187-23=164
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 57 - 34 = 23\)
Ta có bảng sau:
Độ lệch chuẩn: 144
Đồng bằng sông Cửu Long:
15 19 23 24 24 24 26 29 33 33 34 39 42
n=13
Số trung bình: \(\overline X \approx 28,1\)
Trung vị: 26
Tứ phân vị: \({Q_1} = 23,5,{Q_3} = 33,5\)
Mốt là 24 vì có tần số là 3 (xuất hiện 3 lần).
Khoảng biến thiên: R=42-15=27
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 33,5 - 23,5 = 10\)
Ta có bảng sau:
Độ lệch chuẩn: 27,04
b) Số trung bình sai khác vì ở Đồng bằng sông Hồng thì có giá trị bất thường là 187 (cao hơn hẳn giá trị trung bình), còn ở Đồng bằng sông Cửu Long thì không có giá trị bất thường.
Chính giá trị bất thường làm nên sự sai khác đó, còn trung vị không bị ảnh hưởng đến giá trị bất thường nên trung vị ở hai mẫu đều như nhau.
c) Giá trị bất thường ảnh hưởng đến khoảng biến thiên và độ lệch chuẩn, còn với khoảng tứ phân vị thì không (khoảng tứ phân vị đo 50% giá trị ở chính giữa).