K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LN
1
H9
HT.Phong (9A5)
CTVHS
7 tháng 8 2023
a) \(\left(x-3\right)^2+2x-6=0\)
\(\Leftrightarrow x^2-6x+9+2x-6=0\)
\(\Leftrightarrow x^2-4x+3=0\)
\(\Leftrightarrow x^2-x-3x+3=0\)
\(\Leftrightarrow x\left(x-1\right)-3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
b) \(\dfrac{x+3}{x-3}+\dfrac{48}{9-x^2}=\dfrac{x-3}{x+3}\) (ĐKXĐ: \(x\ne\pm3\))
\(\Leftrightarrow\dfrac{x+3}{x-3}-\dfrac{48}{\left(x+3\right)\left(x-3\right)}=\dfrac{x-3}{x+3}\)
\(\Leftrightarrow\dfrac{\left(x+3\right)^2}{\left(x+3\right)\left(x-3\right)}-\dfrac{48}{\left(x+3\right)\left(x-3\right)}=\dfrac{\left(x-3\right)^2}{\left(x+3\right)\left(x-3\right)}\)
\(\Leftrightarrow x^2+6x+9-48=x^2-6x+9\)
\(\Leftrightarrow x^2-x^2+6x+6x+9-9-48=0\)
\(\Leftrightarrow12x-48=0\)
\(\Leftrightarrow12x=48\)
\(\Leftrightarrow x=\dfrac{48}{12}\)
\(\Leftrightarrow x=4\left(tm\right)\)
7 tháng 8 2023
a: (x-3)^2+2x-6=0
=>(x-3)^2+2(x-3)=0
=>(x-3)(x-3+2)=0
=>(x-3)(x-1)=0
=>x=3 hoặc x=1
b:
ĐKXĐ: x<>3; x<>-3
\(\dfrac{x+3}{x-3}+\dfrac{48}{9-x^2}=\dfrac{x-3}{x+3}\)
=>\(\dfrac{\left(x+3\right)^2}{\left(x-3\right)\left(x+3\right)}-\dfrac{48}{\left(x-3\right)\cdot\left(x+3\right)}=\dfrac{\left(x-3\right)^2}{\left(x+3\right)^2}\)
=>(x+3)^2-48=(x-3)^2
=>x^2+6x+9-48=x^2-6x+9
=>6x-39=-6x+9
=>12x=48
=>x=4(nhận)
7 tháng 8 2023
a: \(\dfrac{x}{2}+\dfrac{1-x}{3}>0\)
=>3x+2(1-x)>0
=>3x+2-2x>0
=>x+2>0
=>x>-2
b: (x-9)^2-x(x+9)<0
=>x^2-18x+81-x^2-9x<0
=>-27x+81<0
=>-27x<-81
=>x>3
LN
3
MT
0
24 tháng 7 2018
\(\sin_A=0,8\left(cm\right)\)
\(\Rightarrow\widehat{A}=53^07^'\)
3 tháng 7 2021
\(A=\dfrac{\sqrt{3x-9}}{x}=\sqrt{\dfrac{3x-9}{x^2}}=\sqrt{-\dfrac{9}{x^2}+\dfrac{3}{x}}\)\(=\sqrt{\dfrac{1}{4}-\left(\dfrac{9}{x^2}+2.\dfrac{3}{x}.\dfrac{1}{2}+\dfrac{1}{4}\right)}\)
\(=\sqrt{\dfrac{1}{4}-\left(\dfrac{3}{x}-\dfrac{1}{2}\right)^2}\le\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(\dfrac{3}{x}-\dfrac{1}{2}=0\Leftrightarrow x=6\) (tm)
Vậy \(A_{max}=\dfrac{1}{2}\)
\(B=\dfrac{\sqrt{2x-4}}{x}=\sqrt{\dfrac{2x-4}{x^2}}=\sqrt{-\dfrac{4}{x^2}+\dfrac{2}{x}}=\sqrt{\dfrac{1}{4}-\left(\dfrac{4}{x^2}-2.\dfrac{2}{x}.\dfrac{1}{2}+\dfrac{1}{4}\right)}\)
\(=\sqrt{\dfrac{1}{4}-\left(\dfrac{2}{x}-\dfrac{1}{2}\right)^2}\le\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(\dfrac{2}{x}-\dfrac{1}{2}=0\Leftrightarrow x=4\) (tm)
Vậy \(B_{max}=\dfrac{1}{2}\)
\(C=\dfrac{\sqrt{x-4}}{3x}=\sqrt{\dfrac{x-4}{9x^2}}=\sqrt{-\dfrac{4}{9x^2}+\dfrac{1}{9x}}=\sqrt{\dfrac{1}{144}-\left(\dfrac{4}{9x^2}-2.\dfrac{2}{3x}.\dfrac{1}{12}+\dfrac{1}{144}\right)}\)
\(=\sqrt{\dfrac{1}{144}-\left(\dfrac{2}{3x}-\dfrac{1}{12}\right)^2}\le\sqrt{\dfrac{1}{144}}=\dfrac{1}{12}\)
Dấu "=" xảy ra khi \(x=8\) (tm)
Vậy \(C_{max}=\dfrac{1}{12}\)
TA
0
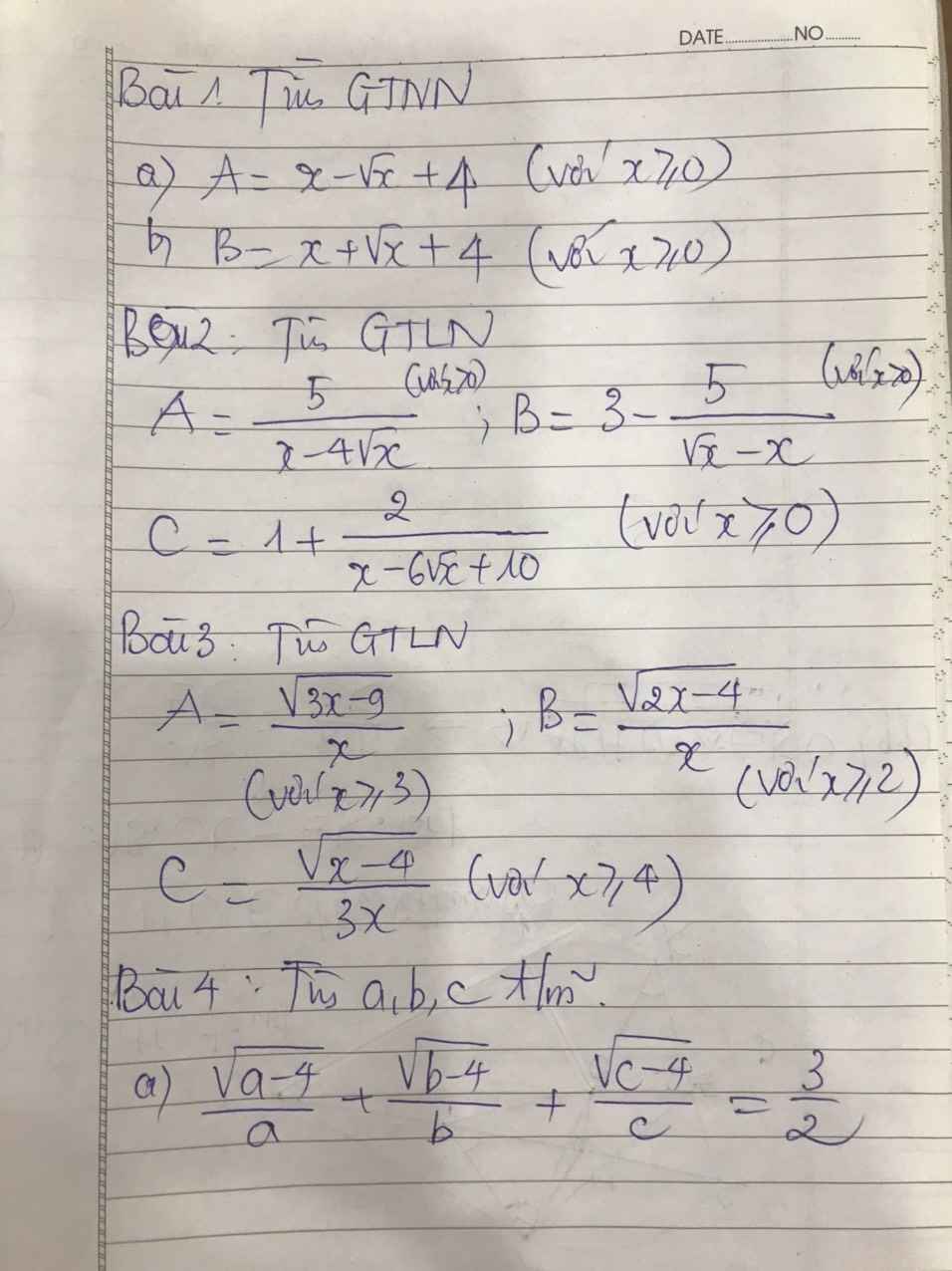
Lời giải:
$(\sqrt{2}-\sqrt{3})^2=(\sqrt{2})^2-2.\sqrt{2}.\sqrt{3}+(\sqrt{3})^2$
$=2-2\sqrt{6}+3=5-2\sqrt{6}$
Bạn chú ý lần sau viết đề bằng công thức toán và viết đúng chính tả.