K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NP
trong các số 11n+1010(n∈N*;n≤1010) có bao nhiêu số là số chính phương
mn giúp mk vs ạ
mk đang cần gấp
0
AH
Akai Haruma
Giáo viên
3 tháng 8 2021
Lời giải:
a. Gọi biểu thức là $A$
\(A=\left[\frac{(1-\sqrt{x})(1+\sqrt{x}+x)}{1-\sqrt{x}}+\sqrt{x}\right].\left[\frac{1-\sqrt{x}}{(1-\sqrt{x})(1+\sqrt{x})}\right]^2\)
\(=(1+\sqrt{x}+x+\sqrt{x}).\frac{1}{(1+\sqrt{x})^2}=(\sqrt{x}+1)^2.\frac{1}{(\sqrt{x}+1)^2}=1\)
Ta có đpcm
b.
\(\sqrt{2012}-\sqrt{2011}=\frac{1}{\sqrt{2012}+\sqrt{2011}}< \frac{1}{\sqrt{2011}+\sqrt{2010}}=\sqrt{2011}-\sqrt{2010}\)
NA
1
H
24 tháng 8 2023
Bài 1:
a)
\(A=\sqrt{2}\left(\sqrt{4.2}-\sqrt{16.2}+3\sqrt{9.2}\right)\\ =\sqrt{2}\left(2\sqrt{2}-4\sqrt{2}+9\sqrt{2}\right)\\ =\sqrt{2}.7\sqrt{2}\\ =7\)
b)
\(B=\dfrac{5\left(\sqrt{6}-1\right)\left(\sqrt{6}-1\right)}{6-1}+\dfrac{\left(\sqrt{2}-\sqrt{3}\right)\left(\sqrt{2}-\sqrt{3}\right)}{2-3}+\sqrt{\sqrt{2}^2-2.\sqrt{2}.\sqrt{1}+\sqrt{1}^2}\\ =\dfrac{5\left(\sqrt{6}-1\right)^2}{5}-\left(\sqrt{2}-\sqrt{3}\right)^2+\sqrt{\left(\sqrt{2}-1\right)^2}\\ =5\left(6-2\sqrt{6}+1\right)-\left(2-2\sqrt{6}+3\right)+\sqrt{2}-1\\ =30-10\sqrt{6}+5-2+2\sqrt{6}-3+\sqrt{2}-1\\ =29-8\sqrt{6}\)
25 tháng 8 2023
2:
a: \(\sqrt{x^2-2x+9}=x+2\)
=>x>=-2 và x^2-2x+9=x^2+4x+4
=>x>=-2 và -2x+9=4x+4
=>x>=-2 và -6x=-5
=>x=5/6(nhận)
b:
ĐKXĐ: x^2-4>=0 và x+2>=0
=>x>=-2 và (x>=2 hoặc x<=-2)
=>x=-2 hoặc x>=2
\(\sqrt{x^2-4}+\sqrt{x+2}=0\)
=>x^2-4=0 và x+2=0
=>x=-2
c:
ĐKXĐ: x>=1
\(\sqrt{x+3-4\sqrt{x-1}}=3\)
=>\(\sqrt{x-1-2\cdot\sqrt{x-1}\cdot2+4}=3\)
=>\(\left|\sqrt{x-1}-2\right|=3\)
=>\(\left[{}\begin{matrix}\sqrt{x-1}-2=3\\\sqrt{x-1}-2=-3\end{matrix}\right.\Leftrightarrow\sqrt{x-1}=5\)
=>x-1=25
=>x=26
d: \(\sqrt{4-8x}-4\sqrt{1-2x}+\sqrt{\dfrac{9-18x}{4}}+1=0\)
=>\(2\sqrt{1-2x}-4\sqrt{1-2x}+\dfrac{3}{2}\sqrt{1-2x}+1=0\)
=>\(1-\dfrac{1}{2}\sqrt{1-2x}=0\)
=>\(\sqrt{1-2x}=2\)
=>1-2x=4
=>2x=-3
=>x=-3/2
24 tháng 7 2021
Bài 3:
a) Thay x=9 vào A, ta được:
\(A=\dfrac{3+2}{3-5}=\dfrac{5}{-2}=\dfrac{-5}{2}\)
b) Ta có: M=B:A
\(=\left(\dfrac{x+3\sqrt{x}}{x-25}+\dfrac{1}{\sqrt{x}-5}\right):\dfrac{\sqrt{x}+2}{\sqrt{x}-5}\)
\(=\dfrac{x+3\sqrt{x}+\sqrt{x}+5}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+2}\)
\(=\dfrac{x+4\sqrt{x}+5}{x+7\sqrt{x}+10}\)
DP
1
27 tháng 12 2021
Bài 2:
c: Để hai đường thẳng song song thì m-1=2
hay m=3
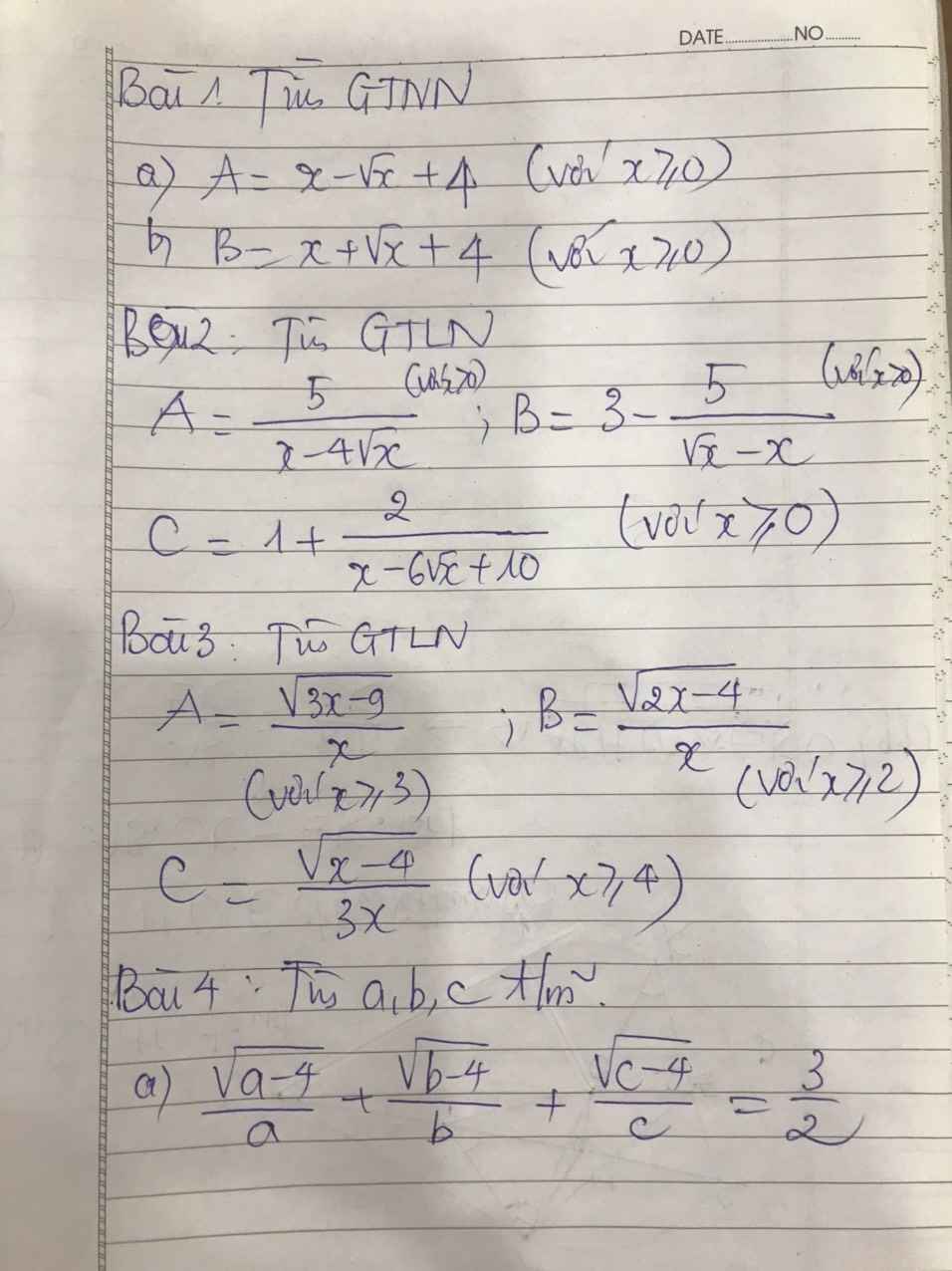
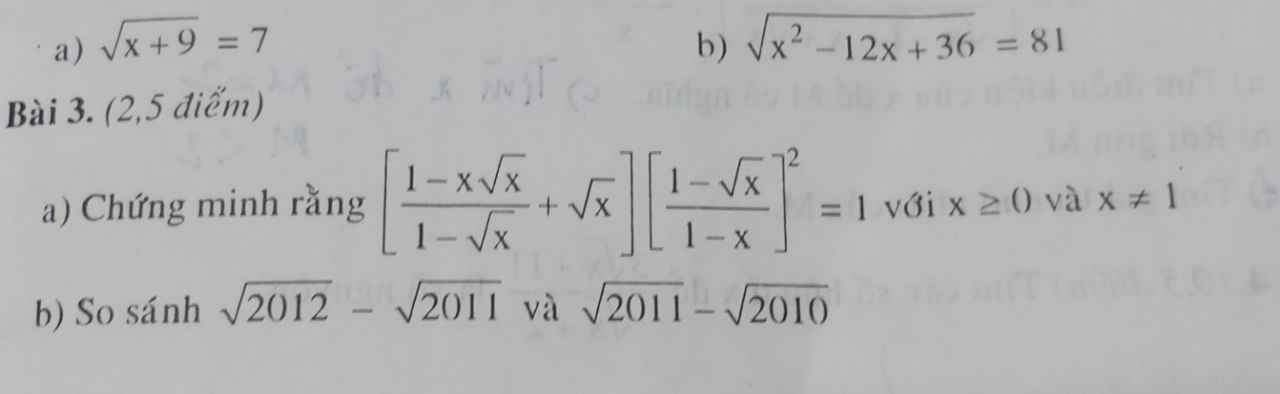
\(A=\dfrac{\sqrt{3x-9}}{x}=\sqrt{\dfrac{3x-9}{x^2}}=\sqrt{-\dfrac{9}{x^2}+\dfrac{3}{x}}\)\(=\sqrt{\dfrac{1}{4}-\left(\dfrac{9}{x^2}+2.\dfrac{3}{x}.\dfrac{1}{2}+\dfrac{1}{4}\right)}\)
\(=\sqrt{\dfrac{1}{4}-\left(\dfrac{3}{x}-\dfrac{1}{2}\right)^2}\le\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(\dfrac{3}{x}-\dfrac{1}{2}=0\Leftrightarrow x=6\) (tm)
Vậy \(A_{max}=\dfrac{1}{2}\)
\(B=\dfrac{\sqrt{2x-4}}{x}=\sqrt{\dfrac{2x-4}{x^2}}=\sqrt{-\dfrac{4}{x^2}+\dfrac{2}{x}}=\sqrt{\dfrac{1}{4}-\left(\dfrac{4}{x^2}-2.\dfrac{2}{x}.\dfrac{1}{2}+\dfrac{1}{4}\right)}\)
\(=\sqrt{\dfrac{1}{4}-\left(\dfrac{2}{x}-\dfrac{1}{2}\right)^2}\le\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(\dfrac{2}{x}-\dfrac{1}{2}=0\Leftrightarrow x=4\) (tm)
Vậy \(B_{max}=\dfrac{1}{2}\)
\(C=\dfrac{\sqrt{x-4}}{3x}=\sqrt{\dfrac{x-4}{9x^2}}=\sqrt{-\dfrac{4}{9x^2}+\dfrac{1}{9x}}=\sqrt{\dfrac{1}{144}-\left(\dfrac{4}{9x^2}-2.\dfrac{2}{3x}.\dfrac{1}{12}+\dfrac{1}{144}\right)}\)
\(=\sqrt{\dfrac{1}{144}-\left(\dfrac{2}{3x}-\dfrac{1}{12}\right)^2}\le\sqrt{\dfrac{1}{144}}=\dfrac{1}{12}\)
Dấu "=" xảy ra khi \(x=8\) (tm)
Vậy \(C_{max}=\dfrac{1}{12}\)
iem cảm ơn !!!!!!<3 cj