Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a=b(mod n) là công thức dùng để chỉ a,b có cùng số dư khi chia cho n, gọi là đồng dư thức
Ta có các tính chất cua đồng dư thức và các tính chất sau:
Cho x là số tự nhiên
Nếu x lẻ thì => x^2 =1 (mod 8)
x^2 =-1(mod 5) hoặc x^2=0(mod 5)
Nếu x chẵn thì x^2=-1(mod 5) hoặc x^2 =1(mod 5) hoặc x^2=0(mod 5)
Vì 2a +1 và 3a+1 là số chính phương nên ta đặt
3a+1=m^2
2a+1 =n^2
=> m^2 -n^2 =a (1)
m^2 + n^2 =5a +2 (2)
3n^2 -2m^2=1(rút a ra từ 2 pt rồi cho = nhau) (3)
Từ (2) ta có (m^2 + n^2 )=2(mod 5)
Kết hợp với tính chất ở trên ta => m^2=1(mod 5); n^2=1(mod 5)
=> m^2-n^2 =0(mod 5) hay a chia hết cho 5
từ pt ban đầu => n lẻ =>n^2=1(mod 8)
=> 3n^2=3(mod 8)
=> 3n^2 -1 = 2(mod 8)
=> (3n^2 -1)/2 =1(mod 8)
Từ (3) => m^2 = (3n^2 -1)/2
do đó m^2 = 1(mod 8)
ma n^2=1(mod 8)
=> m^2 - n^2 =0 (mod 8)
=> a chia hết cho 8
Ta có a chia hết cho 8 và 5 và 5,8 nguyên tố cùng nhau nên a chia hết cho 40.Vậy a là bội của 40

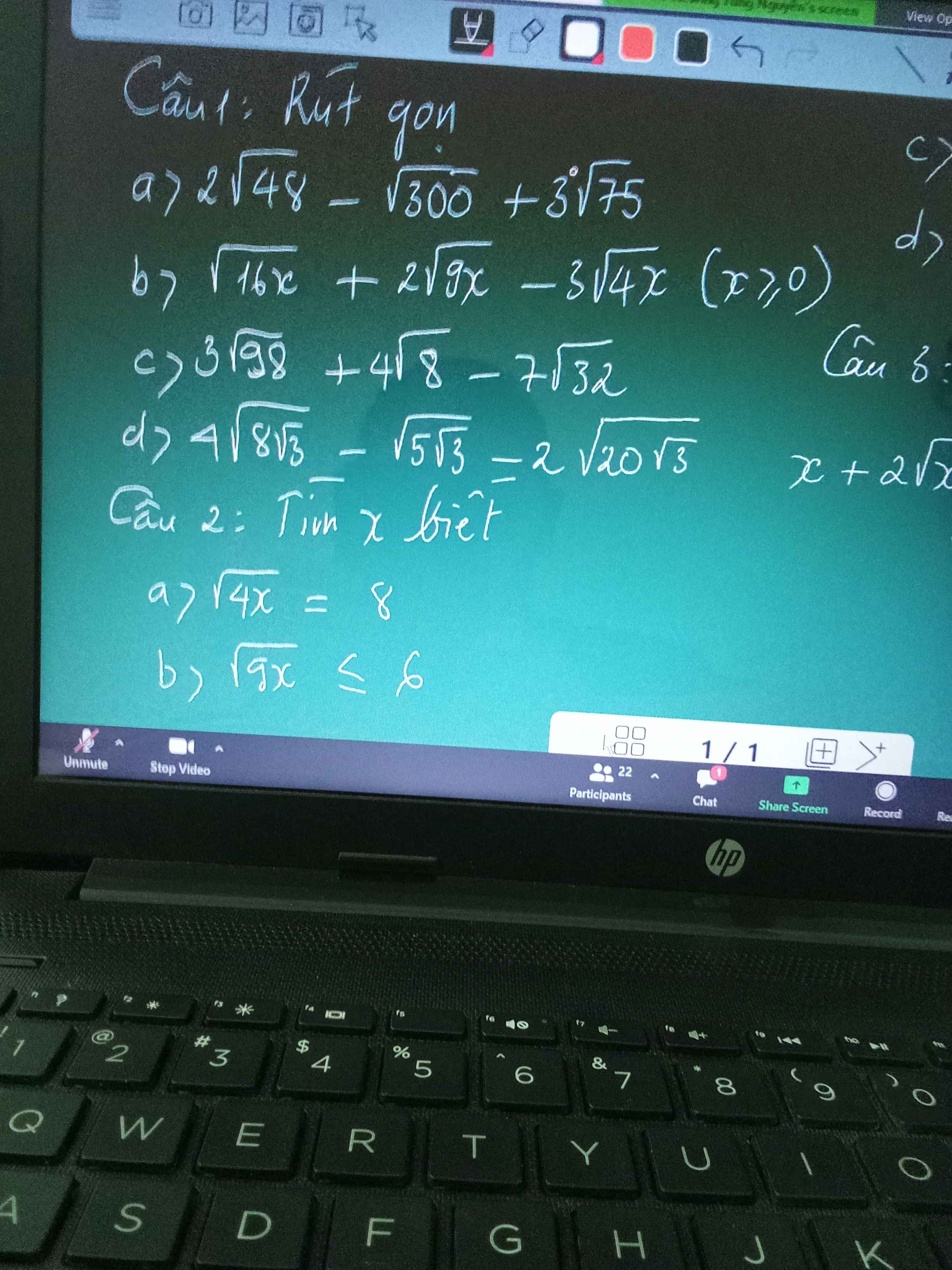
Câu 1
a)=\(8\sqrt{3}-10\sqrt{3}+15\sqrt{3}=13\sqrt{3}\)
b)=\(4\sqrt{x}+6\sqrt{x}-6\sqrt{x}=4\sqrt{x}\)
c)=\(21\sqrt{2}+8\sqrt{2}-28\sqrt{2}=\sqrt{2}\)
d)\(\Rightarrow\)\(8\sqrt{2\sqrt{3}}-\sqrt{5\sqrt{3}}-4\sqrt{5\sqrt{3}}\)
\(\Rightarrow\)\(8\sqrt{2\sqrt{3}}-5\sqrt{5\sqrt{3}}\)
câu 2
a)\(\Rightarrow4x=64\)\(\Rightarrow x=16\)
b)\(\Rightarrow9x\le36\)\(\Rightarrow x\le4\)
Câu 2:
a: Ta có: \(\sqrt{4x}=8\)
\(\Leftrightarrow4x=64\)
hay x=16
b: Ta có: \(\sqrt{9x}\le6\)
\(\Leftrightarrow9x\le36\)
\(\Leftrightarrow x\le4\)
Kết hợp ĐKXĐ, ta được: \(0\le x\le4\)

a: PK=căn 4*9=6cm
MN=4+9=13cm
MP=căn MK*MN=2*căn 13(cm)
NP=căn 9*13=3căn 13(cm)
b: MN=8^2:64/17=17(cm)
NP=căn 17^2-8^2=15(cm)
PK=8*15/17=120/17(cm)
NK=PN^2/NM=225/17(cm)

Lời giải:
$n^5-n=n(n^4-1)=n(n^2-1)(n^2+1)=n(n-1)(n+1)(n^2+1)$
Vì $n,n-1,n+1$ là 3 số nguyên liên tiếp nên tích của chúng chia hết cho $3$
$\Rightarrow n^5-n=n(n-1)(n+1)(n^2+1)\vdots 3$
$\Rightarrow n^5-n+2$ chia $3$ dư $2$. Do đó nó không thể là scp vì scp chia $3$ chỉ có dư $0$ hoặc $1$.