
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A. x = 2
B. \(\dfrac{3}{8}=\dfrac{6}{x}\)\(\Leftrightarrow x=\dfrac{6.8}{3}=16\)
C. x = 3
D. \(x=\dfrac{4.6}{8}=3\)
E. \(x=\dfrac{7}{3}\)
G.\(\dfrac{14}{13}=\dfrac{28}{10-x}\)
<=>\(14\left(10-x\right)=364\)
<=> 10 - x = 26
<=> x = -16
H. \(3\left(x+2\right)=4\left(x-5\right)\)
<=> 3x + 6 = 4x - 20
<=> -x = -26
<=> x = 26
K. \(\dfrac{x}{2}=\dfrac{8}{x}\)
<=> \(x^2=16\)
<=> \(\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
M. \(\left(x-2\right)^2=100\)
<=> \(\left[{}\begin{matrix}x-2=10\\x-2=-10\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=12\\x=-8\end{matrix}\right.\)
a=2
b=16
c=3
d=3
mik chỉ biết thế này thôi(ko chắc đúng=3)

\(\frac{3^{10}.\left(-5\right)^{21}}{\left(-5\right)^{20}.3^{12}}=\frac{3^{10}.\left(-5\right)^{20}.\left(-5\right)}{\left(-5\right)^{20}.3^{10}.3^2}=\frac{-5}{3^2}=-\frac{5}{9}\)

\(\dfrac{2n+15}{n+1}\in Z\Rightarrow2n+15⋮n+1\)
\(\Rightarrow2n+15-2\left(n+1\right)⋮n+1\)
\(\Rightarrow13⋮n+1\)
\(\Rightarrow n+1=Ư\left(13\right)\)
\(\Rightarrow n+1=\left\{-13;-1;1;13\right\}\)
\(\Rightarrow n=\left\{-14;-2;0;12\right\}\)
Cách hai: Theo bezout ta có: \(\dfrac{2n+15}{n+1}\) \(\in\) Z ⇔ 2.(-1) + 15 ⋮ n +1
⇔ 13 ⋮ n +1 ⇒ n + 1 \(\in\) { -13; -1; 1; 13} ⇒ n \(\in\) { -14; -2; 0; 12}


a) Ta có x.y = 6 và x > y. Với x > y, ta có thể giải quyết bài toán bằng cách thử các giá trị cho x và tìm giá trị tương ứng của y. - Nếu x = 6 và y = 1, thì x.y = 6. Điều này không thỏa mãn x > y. - Nếu x = 3 và y = 2, thì x.y = 6. Điều này thỏa mãn x > y. Vậy, một giải pháp cho phương trình x.y = 6 với x > y là x = 3 và y = 2. b) Ta có (x-1).(y+2) = 10. Mở ngoặc, ta có x.y + 2x - y - 2 = 10. Từ phương trình ban đầu (x.y = 6), ta có 6 + 2x - y - 2 = 10. Simplifying the equation, we get 2x - y + 4 = 10. Tiếp tục đơn giản hóa, ta có 2x - y = 6. c) Ta có (x + 1).(2y + 1) = 12. Mở ngoặc, ta có 2xy + x + 2y + 1 = 12. Từ phương trình ban đầu (x.y = 6), ta có 2(6) + x + 2y + 1 = 12. Simplifying the equation, we get 12 + x + 2y + 1 = 12. Tiếp tục đơn giản hóa, ta có x + 2y = -1. Vậy, giải pháp cho các phương trình là: a) x = 3, y = 2. b) x và y không có giá trị cụ thể. c) x và y không có giá trị cụ thể.

x-3/-9 = -4/x-3
(x-3)^2=-9.-4=36
=>TH1 x-3= 6
TH2 x-3 = -6
=> TH1: X= 9
TH2: X=-3

Ta có: \(\left(x+5\right)\left(y-3\right)=15\)
Vì \(x,y\) nguyên nên \(x+5\) và \(y-3\) có giá trị nguyên
\(\Rightarrow x+5;y-3\) là các ước của \(15\)
Ta có bảng sau:
| x + 5 | 1 | 3 | 5 | 15 | -1 | -3 | -5 | -15 |
| y - 3 | 15 | 5 | 3 | 1 | -15 | -5 | -3 | -1 |
| x | -4 | -2 | 0 | 10 | -6 | -8 | -10 | -20 |
| y | 18 | 8 | 6 | 4 | -12 | -2 | 0 | 2 |
Vì \(x,y\) nguyên nên ta được:
\(\left(x,y\right)=\left\{\left(-4;18\right);\left(-2;8\right);\left(0;6\right);\left(10;4\right);\left(-6;-12\right);\left(-8;-2\right);\left(-10;0\right);\left(-20;2\right)\right\}\)
Vậy: ...
(\(x\) + 5).(y - 3) = 15
Ư(15) = {-15; -5; -3; -1; 1; 3; 5; 15}
Lập bảng ta có:
| \(x\) + 5 | -15 | -5 | -3 | -1 | 1 | 3 | 5 | 15 |
| \(x\) | -20 | -10 | -8 | -6 | -4 | -2 | 0 | 10 |
| y - 3 | -1 | -3 | -5 | -15 | 15 | 5 | 3 | 1 |
| y | 2 | 0 | -2 | -12 | 18 | 8 | 6 | 4 |
Theo bảng trên ta có:
(\(x\); y) = (-20; 2); (-10; 0); (-8; -2); (-6; -12); (-4; 18); (0; 6); (10; 4)

Số dư lớn nhất trong 1 phép chia bằng số chia -1
=> số dư lớn nhất trong phép chia trên = 5-1=4
Theo đề bài số dư = {2;4}
Với số dư = 2 thì thương là 2:2=1
=>x=5x1+2=7
Với số dư = 4 thì thương là 4:2=2
=> x=5x2+4=14
Theo đề :
\(x=5.r+2.r\)
mà \(2.r< 5\Rightarrow r\in\left\{1;2\right\}\Rightarrow x\in\left\{7;14\right\}\)
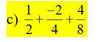
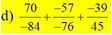
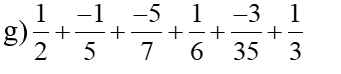 giúp mik với, đang gấp, bạn nào nhanh mình đánh giá cao ạ
giúp mik với, đang gấp, bạn nào nhanh mình đánh giá cao ạ 
X-15=-10
=> X=5.
5 đúng k nhỉ