PK
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
1 tháng 9 2023
Bài 1
a, cm : A = 165 + 215 ⋮ 3
A = 165 + 215
A = (24)5 + 215
A = 220 + 215
A = 215.(25 + 1)
A = 215. 33 ⋮ 3 (đpcm)
b,cm : B = 88 + 220 ⋮ 17
B = (23)8 + 220
B = 216 + 220
B = 216.(1 + 24)
B = 216. 17 ⋮ 17 (đpcm)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
1 tháng 9 2023
c, cm: C = 1 - 2 + 22 - 23 + 24 - 25 + 26 -...-22021 + 22022 : 6 dư 1
C=1+(-2+22-23+24- 25+26)+...+(-22017+22018-22019+22020-22021+22022)
C = 1 + 42 +...+ 22016.(-2 + 22 - 23 + 24 - 25 + 26)
C = 1 + 42+...+ 22016.42
C = 1 + 42.(20+...+22016)
42 ⋮ 6 ⇒ C = 1 + 42.(20+...+22016) : 6 dư 1 đpcm
VN
1
27 tháng 8 2023
\(S=1+2+2^2+2^3+2^4+...+2^{2011}\)
\(\Rightarrow S=\left(1+2+2^2\right)+2^3\left(1+2+2^2\right)+...+2^{2009}\left(1+2+2^2\right)\)
\(\Rightarrow S=7+2^3.7+...+2^{2009}.7\)
\(\Rightarrow S=7\left(1+2^3+...+2^{2009}\right)⋮7\)
\(\Rightarrow dpcm\)
CM
2 tháng 5 2019
a, 2.(x – 5)+7 = 77
<=> 2.(x – 5) = 70 <=> x – 5 = 35 <=> x = 40
b, x - 1 3 - 3 5 : 3 4 + 2 . 2 3 = 14
<=> x - 1 3 - 3 + 2 4 = 14
<=> x - 1 3 = 14 + 3 - 16 = 1
<=> x – 1 = 1 <=> x = 2
c, 1 + 2 + 2 2 + 2 3 + . . . + 2 2016 = 2 x - 1 - 1
Đặt: A = 1 + 2 + 2 2 + 2 3 + . . . + 2 2016 => 2A = 2 + 2 2 + 2 3 + . . . + 2 2017
=> 2A – A = ( 2 + 2 2 + 2 3 + . . . + 2 2017 ) – ( 1 + 2 + 2 2 + 2 3 + . . . + 2 2016 )
=> A = 2 2017 - 1
Ta có: 1 + 2 + 2 2 + 2 3 + . . . + 2 2016 = 2 x - 1 - 1 => 2 2017 - 1 = 2 x - 1 - 1 => x = 2018
d, 5 2 x - 3 - 2 . 5 2 = 5 2 . 3
<=> 5 2 x - 3 = 5 2 . 3 + 5 2 . 2
<=> 5 2 x - 3 = 5 2 . ( 3 + 2 )
<=> 5 2 x - 3 = 5 3
<=> 2x – 3 = 3 => x = 3
PT
1
CM
19 tháng 4 2018
Ta có
2 1 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 +...+ 2 98 + 2 99 + 2 100
= 2 1 + ( 2 2 + 2 3 + 2 4 ) + ( 2 5 + 2 6 + 2 7 ) +...+ ( 2 98 + 2 99 + 2 100 )
= 2 + 2 2 1 + 2 + 2 2 + 2 5 1 + 2 + 2 2 + . . . + 2 98 1 + 2 + 2 2
= 2 + 2 2 . 7 + 2 5 . 7 + . . . + 2 98 . 7 = 2 + 7 2 2 + 2 5 + . . . + 2 98
Mà 7 . 2 2 + 2 5 + . . . + 2 98 ⋮ 7
Nên 2 + 7 2 2 + 2 5 + . . . + 2 98 : 7 d ư 2
PT
1
NH
0
VV
3
T
19 tháng 10 2023
\(A=2+2^2+2^3+...+2^{2020}+2^{2021}+2^{2022}\\=(2+2^2)+(2^3+2^4)+(2^5+2^6)+...+(2^{2021}+2^{2022})\\=2\cdot(1+2)+2^3\cdot(1+2)+2^5\cdot(1+2)+...+2^{2021}\cdot(1+2)\\=2\cdot3+2^3\cdot3+2^5\cdot3+...+2^{2021}\cdot3\\=3\cdot(2+2^3+2^5+..+2^{2021})\)
Vì \(3\cdot\left(2+2^3+2^5+...+2^{2021}\right)⋮3\)
nên \(A⋮3\).
\(Toru\)
TN
19 tháng 10 2023
A=(2+22)+22(2+22)+...+22020(2+22)
A= 6.1+22.6+...+22020.6
A=6(1+22+...+22020) chia hết cho 3
vậy A chia hết cho 3
LT
1
3 tháng 9 2023
\(A=2^1+2^2+2^3+...+2^{2016}\)
\(\Rightarrow A=2\left(1+2^1+2^2\right)+2^4\left(1+2^1+2^2\right)...+2^{2014}\left(1+2^1+2^2\right)\)
\(\Rightarrow A=2.7+2^4.7...+2^{2014}.7\)
\(\Rightarrow A=7\left(2+2^4...+2^{2014}\right)⋮7\)
\(\Rightarrow dpcm\)
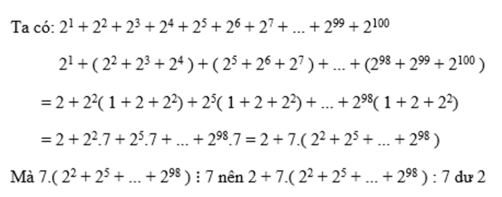
a/
\(2C=2+2^2+2^3+..+2^{2017}+2^{2018}\)
\(C=2C-C=2^{2018}-1\)
b/
\(\frac{2^{2021}}{C}=\frac{2^{2021}}{2^{2018}-1}=\frac{2^3.2^{2018}-2^3+2^3}{2^{2018}-1}=8+\frac{8}{2^{2018}-1}\)
Số dư là 8