
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


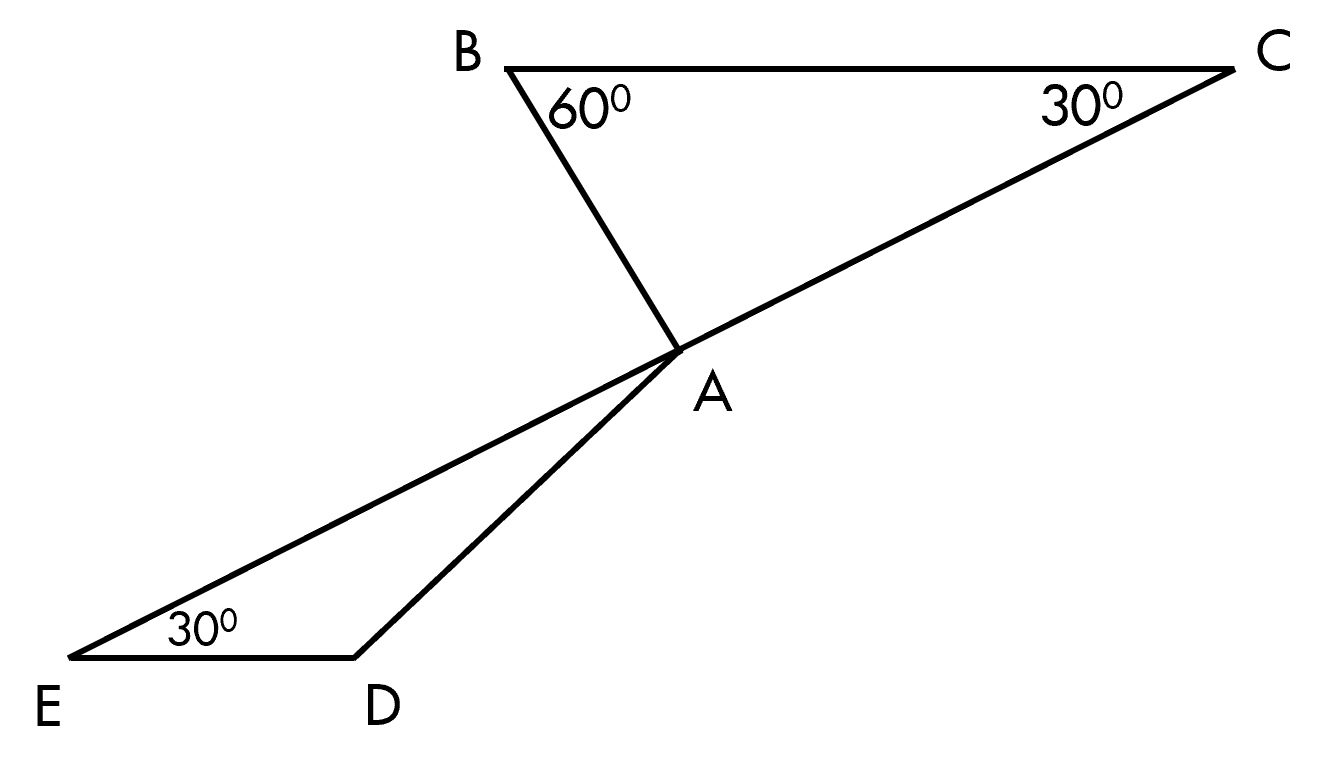
Xét ∆ABC và ∆DBC có:
AB = BD
Góc ABC = góc CBD
Góc BAC = góc BDC
=> ∆ABC = ∆DBC

a/
\(\widehat{BCE}=\widehat{CED}=30^o\)
Hai góc trên ở vị trí sole trong => BC//DE
b/
Ta có
BC//DE (cmt) \(\Rightarrow\widehat{AFB}=180^o-\widehat{EDF}\) (Hai góc trong cùng phía bù nhau)
\(\Rightarrow\widehat{AFB}=180^o-135^o=45^o\)

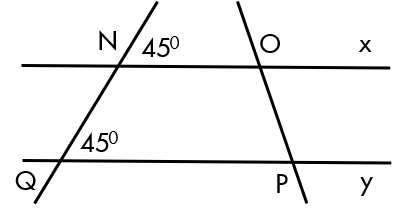
ta có góc QNO = 1800 - 450 = 1350
vì tổng 4 góc của một tứ giác bằng 3600
xét tứ giác QNOP
ta có góc NOP + góc QPO = 3600 - ( 450 + 1350) = 1800 (đpcm)

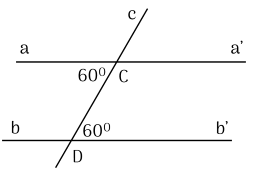
Ta có: góc aCd = góc CDb' (=60°)
Mà 2 góc này ở vị trí so le trong
=> aa' // bb'

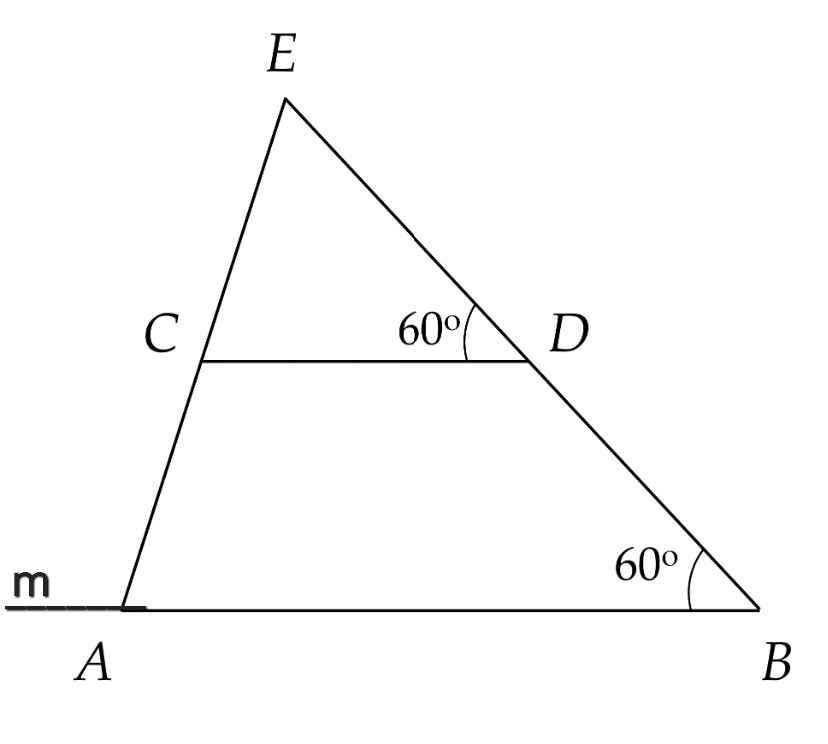
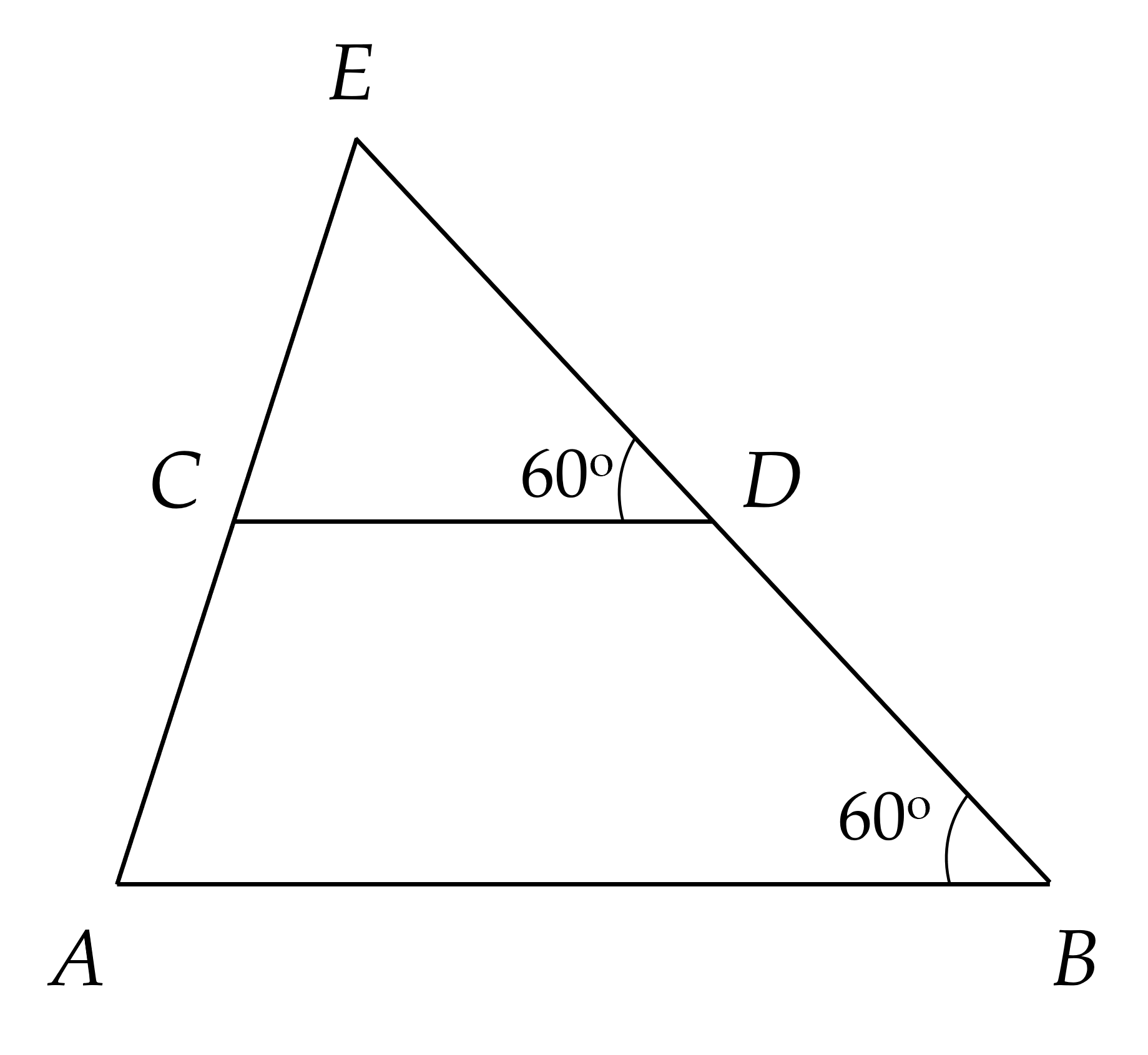
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰

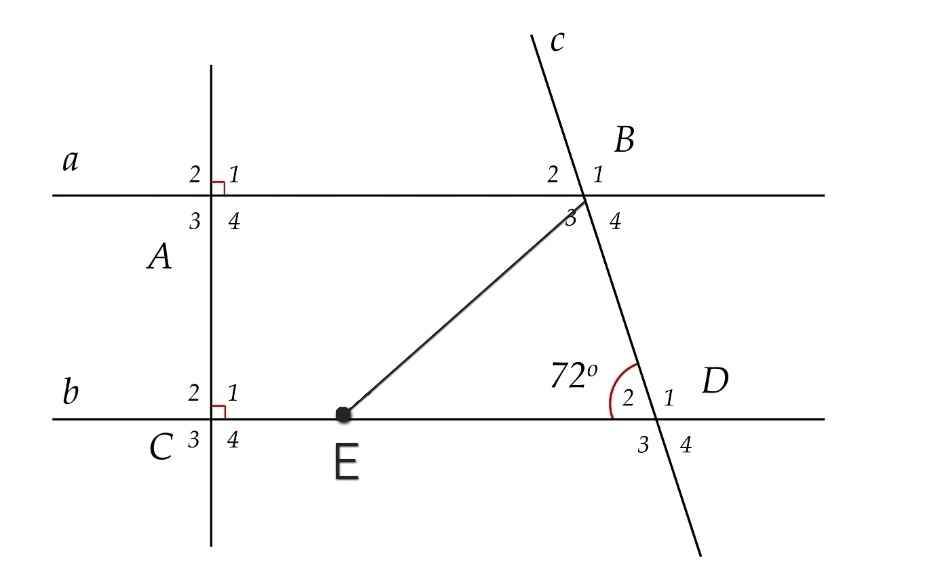 a) Ta có:
a) Ta có:
∠A₁ = ∠C₁ = 90⁰
Mà ∠A₁ và ∠C₁ là hai góc đồng vị
⇒ a // b
b) Ta có:
∠D₁ + ∠D₂ = 180⁰ (kề bù)
⇒ ∠D₁ = 180⁰ - ∠D₂
= 180⁰ - 72⁰
= 108⁰
Do a // b (cmt)
⇒ ∠ABD = ∠D₁ = 108⁰ (so le trong)
c) Do BE là tia phân giác của ∠ABD
⇒ ∠ABE = ∠ABD : 2
= 108⁰ : 2
= 54⁰

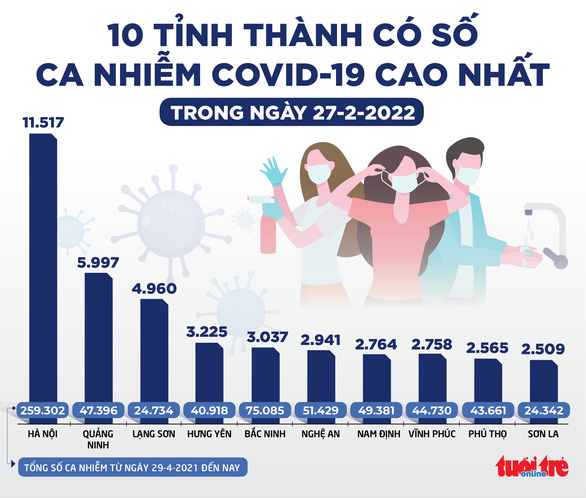
a. Những tỉnh thành phố có ca nhiễm hơn 2800 ca: Nghệ An, Bắc Ninh, Hưng Yên, Lạng Sơn, Quảng Ninh, Hà Nội.
b. Tỉnh có số ca nhiễm Covid 19 cao nhất là: Hà Nội

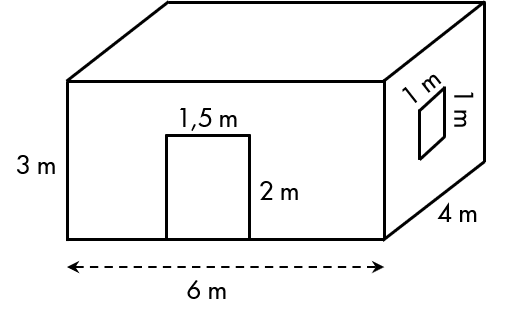
Diện tích cửa ra vào hình chữ nhật là:
2 x 1,5 = 3 (m2)
Diện tích của sổ hình vuông là :
1 x 1 = 1 (m2)
Diện tích xung quanh của căn phòng là :
2 x 3 x ( 6 +4) = 60 (m2)
Nếu chỉ quét sơn mặt ngoài của bốn bức tường xung căn phòng ( không sơn cửa ) thì diện tích cần quét sơn là:
60 - 3 - 1 = 56 (m2)
Số Tiền anh Đông cần trả để quét mặt ngoài của 4 bức tường xung căn phòng ( không sơn cửa ) là :
35 000 x 56 = 1 960 000 (đồng)
Nếu quét sơn cả mặt trong và mặt ngoài của 4 bức tường xung quanh căn phòng (không sơn cửa) thì anh Đông cần trả số tiền là:
1 960 000 x 2 = 3 920 000 (đồng)
kết luận
Diện tích bốn bức tường là diện tích xung quanh của một hình hộp chữ nhật có chiều cao 33 m; chiều dài và chiều rộng của đáy lần lượt là 66 m và 44 m.
Diện tích bốn bức tường là: 3.2.(4+6)=603.2.(4+6)=60 m22.
Diện tích cửa là: 1,5.2+12=41,5.2+12=4 m22.
Diện tích tường cần sơn là 60−4=5660−4=56 m22.
Số tiền anh Đông cần để sơn bức tường là: 56.3556.35 000=1000=1 960960 000000 đồng hay 1,961,96 triệu đồng.


Ta có:
Nếu bóng của hai cột đèn bằng nhau, tức là BC = EF
Suy ra, ABC = DEF (g.c.g)
Từ đó ta có AB = DE (hai cạnh tương ứng)
Vậy khi bóng của hai cột đèn bằng nhau thì độ dài hai cột bằng nhau

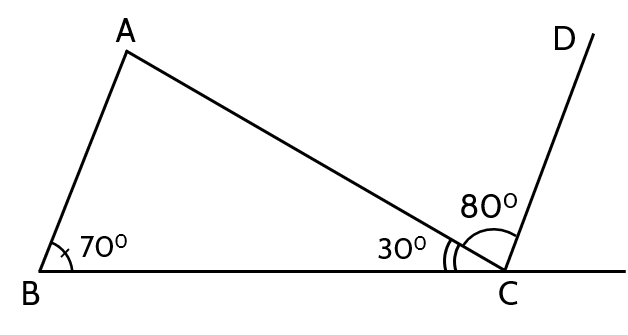




Xét tg ABC có
\(\widehat{BAC}=180^o-\widehat{ABC}-\widehat{ACB}\) (tổng các góc trong của 1 tg \(=180^o\) )
\(\Rightarrow\widehat{BAC}=180^o-70^o-30^o=80^o=\widehat{ACD}\)
Hai góc \(\widehat{BAC}=\widehat{ACD}\) ở vị trí so le trong => AB//CD