Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

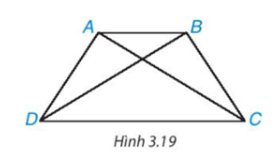
Vì ABCD là hình thang cân (AC // CD) nên AD = BC; \(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}\)
Xét ∆ACD và ∆BDC có
AD = BC (chứng minh trên);
\(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}\) (chứng minh trên);
Cạnh CD chung.
Do đó ∆ACD = ∆BDC (c.g.c).
Suy ra AC = BD (hai góc tương ứng).

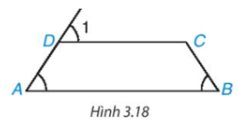
Ta có \(\widehat A = \widehat {{D_1}}\) mà hai góc này ở vị trí đồng vị nên AB // CD.
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có \(\widehat A = \widehat B\) nên ABCD là hình thang cân.
Do đó AD = BC (đpcm).

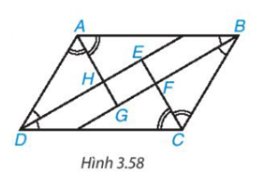
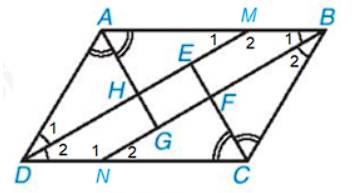
Vì tứ giác ABCD là hình bình hành nên AB // CD hay AM // DN.
Suy ra \(\widehat {{M_1}} = \widehat {{D_2}}\)(hai góc so le trong)
Mà \(\widehat {{D_1}} = \widehat {{D_2}}\) (vì DM là tia phân giác \(\widehat {A{\rm{D}}C}\)).
Do đó \(\widehat {{M_1}} = \widehat {{D_1}}\) nên tam giác ADM cân tại A.
Chứng minh tương tự, ta có tam giác BCN cân tại C.
Vì \(\widehat {{B_1}} = \widehat {{B_2}};\widehat {{D_1}} = \widehat {{D_2}}\) (vì DM, BN lần lượt là tia phân giác của \(\widehat {A{\rm{D}}C};\widehat {ABC}\)).
Mà \(\widehat {A{\rm{D}}C} = \widehat {ABC}\) (vì tứ giác ABCD là hình bình hành).
Do đó \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{D_1}} = \widehat {{D_2}}\)
Tam giác ADM cân tại A, tam giác BCN cân tại C.
Mà \(\widehat {{B_1}} = \widehat {{D_2}}\)nên \(\widehat {{M_1}} = \widehat {{N_2}}\)suy ra \(\widehat {{M_1}} = \widehat {{N_2}}\)
Tứ giác BMDN có \(\widehat {{B_1}} = \widehat {{D_2}};\widehat {{M_2}} = \widehat {{N_1}}\) nên tứ giác BMDN là hình bình hành.
Suy ra DM // BN hay HE // GF.
Tam giác ADM cân tại A có AH là đường phân giác nên AH cũng là đường cao.
Suy ra \(\widehat {AHE} = {90^o}\) nên \(\widehat {EHG} = {90^o}\)
Mà HE // GF suy ra \(\widehat {AGF} = {90^o}\) (hai góc đồng vị).
Tương tự, ta cũng chứng minh được: \[\widehat {HEF} = {90^o};\widehat {GF{\rm{E}}} = {90^o}\]
Tứ giác EFGH có \(\widehat {EHG} = {90^o};\widehat {AGF} = {90^o};\widehat {{\rm{HEF}}} = {90^o}\)
Do đó tứ giác EFGH là hình chữ nhật.

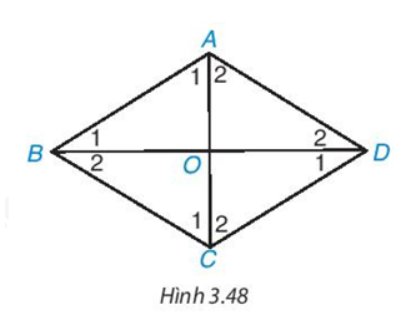
a) Vì tứ giác ABCD là hình thoi nên AB = AD.
Suy ra ∆ABD có cân tại A.
b) Vì tứ giác ABCD là hình thoi nên AB = BC = CD = DA.
Xét ∆ABC và ∆ADC có:
AB = AD (chứng minh trên);
BC = CD (chứng minh trên);
Cạnh AC chung.
Do đó ∆ABC = ∆ADC (c.c.c)
Suy ra \(\)\(\widehat {{A_1}} = \widehat {{A_2}}\)(hai góc tương ứng)
Hay AC là đường phân giác của góc A.
Tam giác ABD cân tại A có AO là đường phân giác của góc A (vì AC là đường phân giác góc A) nên AO cũng là đường cao.
Khi đó AO ⊥ BD hay AC ⊥ BD.
Vậy AC vuông góc với BD và AC là đường phân giác của góc A.

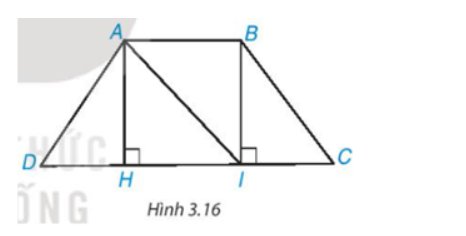
a) Vì ABCD là hình thang cân (AB // CD) nên \(\widehat {BAI} = \widehat {AIH}\)(hai góc so le trong).
Ta có AH ⊥ DC, BI ⊥ DC suy ra AH // BI.
Do đó \(\widehat {AIB} = \widehat {HAI}\) (hai góc so le trong).
Xét ∆AHI và ∆IBA có:
\(\widehat {BAI} = \widehat {AIH}\) (chứng minh trên);
Cạnh AI chung;
\(\widehat {AIB} = \widehat {HAI}\) (hai góc so le trong).
Do đó ∆AHI = ∆IBA (c.g.c).
Suy ra AH = BI (hai cạnh tương ứng).
b) Vì ABCD là hình thang cân (AC // CD) nên \(\widehat C = \widehat D\).
Vì ∆AHD và ∆BIC có:
\(\widehat {AH{\rm{D}}} = \widehat {BIC} = {90^o}\) và \(\widehat C = \widehat D\) nên \(90^o - \widehat C = 90^o - \widehat {BIC} \Leftrightarrow \widehat {DAH} = \widehat {CBI}\)
Xét ∆AHD và ∆BIC có:
\(\widehat {AH{\rm{D}}} = \widehat {BIC} = {90^o}\) (vì AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD);
\(AH = BI\) (chứng minh trên
\(\widehat {DAH} = \widehat {CBI}\) (chứng minh trên).
Do đó ∆AHD = ∆BIC (góc - cạnh - góc).
Suy ra AD = BC (hai cạnh tương ứng).

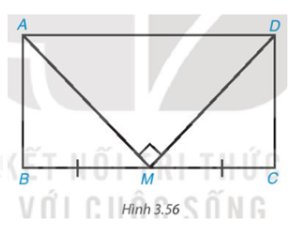
Do ABCD là hình chữ nhật nên \(\left\{{}\begin{matrix}AB=CD\\AD=BC\end{matrix}\right.\)
Mà M là trung điểm BC ⇒ \(\left\{{}\begin{matrix}MA=MD\\MB=MC\end{matrix}\right.\) (1)
Áp dụng định lí Py-ta-go trong tam giác ABM, MCD, AMD, ta có:
\(\left\{{}\begin{matrix}AB^2+MB^2=AM^2\\CD^2+MC^2=MD^2\\AM^2+MD^2=AD^2\end{matrix}\right.\) (2)
Từ (1) và (2), ta có:
\(2AB^2+2BM^2=AD^2=BC^2=4BM^2\)
\(\Rightarrow AB=BM=\dfrac{1}{2}BC\)
Mà \(2\cdot\left(AB+BC\right)=36\)
⇒ AB = 6 (cm) và BC = 12 (cm).

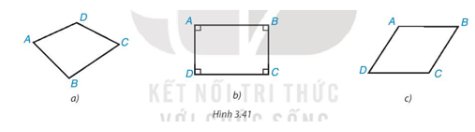
Tứ giác ABCD trong Hình 3.41b là hình chữ nhật vì có \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)
Tứ giác ABCD trong Hình 3.41a và Hình 3.41c không phải là hình chữ nhật vì không có 4 góc vuông.

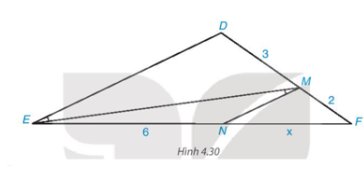
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).

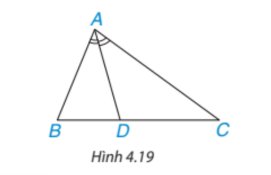
Dựa vào tính chất đường phân giác trong tam giác với tam giác ABC có AD là phân giác của góc \(\widehat{BAC}\) , ta được: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\).
Xét tam giác DBC, ta có:
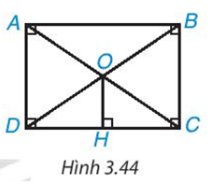
O là trung điểm cạnh BD (tính chất hình chữ nhật)
OH // BC (cùng vuông góc với CD)
⇒ OH là đường trung bình tam giác BCD.
⇒ H là trung điểm của CD (đpcm).