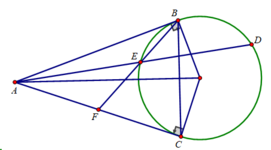
Cho đường tròn (O). Từ điểm A bên ngoài đường tròn vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Đường thẳng kẻ qua C song song với AB cắt đường tròn (O) ở D, AD cắt đường tròn (O) ở M, CM cắt AB ở N. Chứng minh: a) Góc BAD = Góc ACN b) AN2 = NM.NC; c) N là trung điểm của AB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 3 2021
a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
14 tháng 5 2023
a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB^2=AE*AD
13 tháng 4 2021
a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
12 tháng 4 2023
c: góc BDC=1/2*góc BOC=60 độ
BD//AC
=>góc DCx=góc BDC=60 độ(so le trong)
=>góc ODC=góc OCD=90-60=30 độ
góc BDO=góc CDO=30 độ
=>góc BOD=góc COD=120 độ
=>ΔBOD=ΔCOD
=>BD=CD
=>D nằm trên trung trực của BC
=>A,O,D thẳng hàng
ai đó làm dùng cái tôi cũng đang cần bài này :((