Mn chỉ mik vs
Giải hệ pt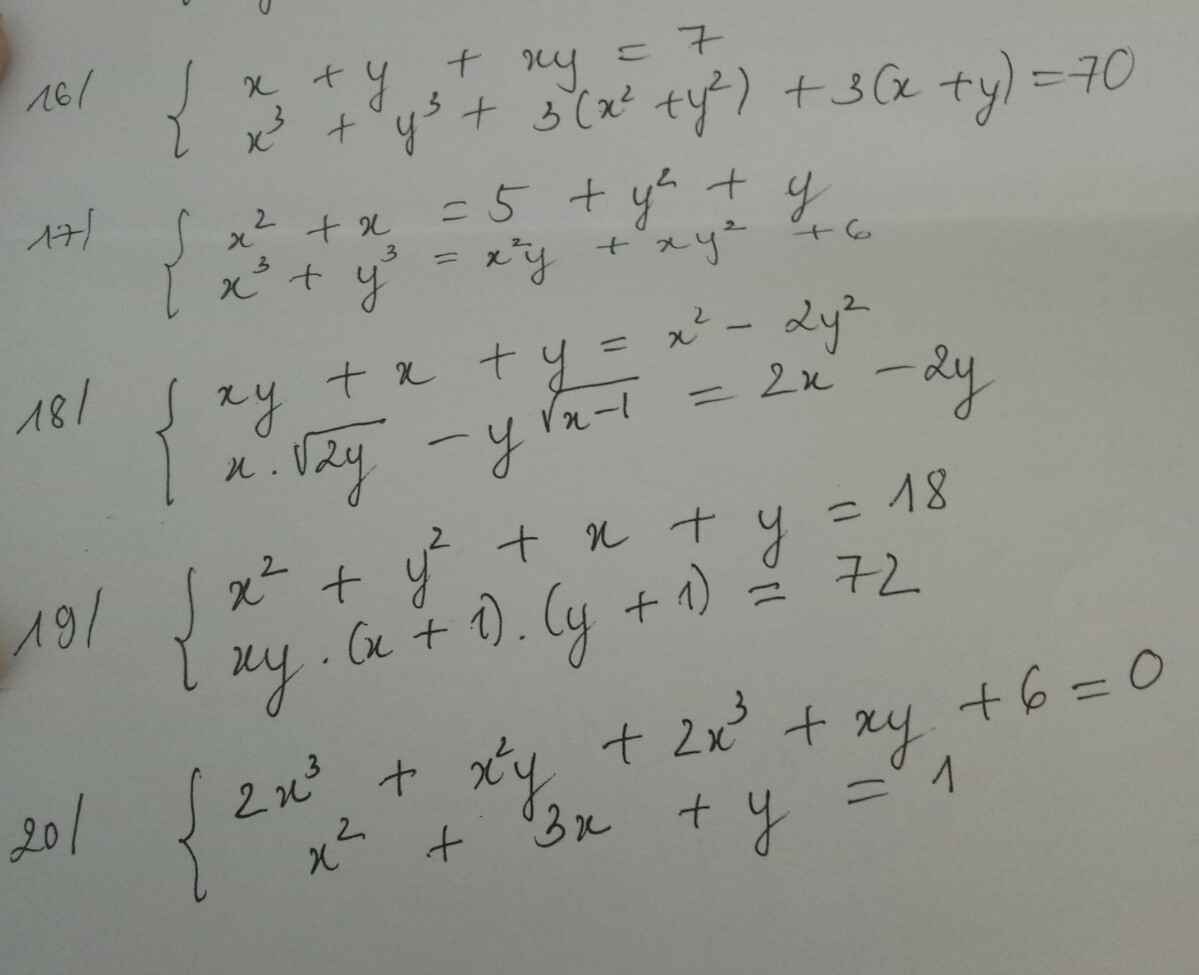
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐK: \(-1\le x\le1\)
Đặt \(\sqrt{1-x}=a;\sqrt{x+1}=b\Rightarrow3-x=2a^2+b^2\)
\(pt\Leftrightarrow2a-b+3ab=2a^2+b^2\)
\(\Leftrightarrow2a^2+b^2-2a+b-3ab=0\)
\(\Leftrightarrow2a^2-a\left(3b+2\right)+b^2+b=0\)
\(\Delta=\left(3b+2\right)^2-4.2.\left(b^2+b\right)=9b^2+12b+4-8b^2-8b\)
\(=b^2+4b+4=\left(b+2\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}a=\dfrac{3b+2-\left(b+2\right)}{4}=\dfrac{2b}{4}=\dfrac{b}{2}\Leftrightarrow2a=b\left(1\right)\\a=\dfrac{3b+2+b+2}{4}=\dfrac{4b+4}{4}=b+1\left(2\right)\end{matrix}\right.\)
pt (1) \(\Leftrightarrow2\sqrt{1-x}=\sqrt{x+1}\)
\(\Leftrightarrow4\left(1-x\right)=x+1\)
\(\Leftrightarrow5x=3\Leftrightarrow x=\dfrac{5}{3}\left(tm\right)\)
\(pt\left(2\right)\Leftrightarrow\sqrt{1-x}=1+\sqrt{x+1}\)
\(\Leftrightarrow1-x=1+x+1+2\sqrt{x+1}\)
\(\Leftrightarrow-1-2x=2\sqrt{x+1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\4x^2+4x+1=4x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\4x^2=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\left(l\right)\\x=-\dfrac{\sqrt{3}}{2}\left(tm\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy, pt có tập nghiệm là: \(S=\left\{-\dfrac{\sqrt{3}}{2};\dfrac{5}{3}\right\}\)

em ơi chưa có bài em nhé, em chưa tải bài lên lám sao mình giúp được

HPT : \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{5}{36}\\\frac{4}{x}+\frac{3}{y}=\frac{1}{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{3}{x}+\frac{3}{y}=\frac{5}{12}\left(1\right)\\\frac{4}{x}+\frac{3}{y}=\frac{1}{2}\left(2\right)\end{cases}}\)
Từ (1) và (2), lấy vế trừ vế ta được :
\(\Leftrightarrow\left(\frac{4}{x}+\frac{3}{y}\right)-\left(\frac{3}{x}+\frac{3}{y}\right)=\frac{1}{2}-\frac{5}{12}\)
\(\Leftrightarrow\frac{1}{x}=\frac{1}{12}\)
\(\Leftrightarrow\frac{1}{y}=\frac{5}{36}-\frac{1}{x}=\frac{5}{36}-\frac{1}{12}=\frac{1}{18}\)
\(\Leftrightarrow\hept{\begin{cases}x=12\\y=18\end{cases}}\)

\(\left\{{}\begin{matrix}3x+1< x-7\\1-2x>x+1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x< -8\\3x< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< -4\\x< 0\end{matrix}\right.\) \(\Rightarrow x< -4\)
Vậy nghiệm của hệ là \(S=\left(-\infty;-4\right)\)


\(\dfrac{x+3}{x-3}-\dfrac{x-3}{x+3}=\dfrac{9}{x^2-9}\left(ĐKXĐ:x\ne\pm3\right)\)
\(\Leftrightarrow\dfrac{\left(x+3\right)^2-\left(x-3\right)^2}{\left(x-3\right)\left(x+3\right)}=\dfrac{9}{\left(x-3\right)\left(x+3\right)}\)
\(\Rightarrow x^2+6x+9-x^2+6x-9=9\)
\(\Leftrightarrow12x=9\)
\(\Leftrightarrow x=\dfrac{3}{4}\) (nhận).
Vậy \(S=\left\{\dfrac{3}{4}\right\}\)

Bài này quá dễ
x/40 - x/50= 1/3
<=>5x/200 - 4x/200=1/3
<=> x/200= 1/3
<=> x= 200/3.
bạn ê, mik bị ngu toán, lười suy nghĩ ấy mà nên đừng nói dễ hay khó j vs mik

a) \(\left(x+1\right)^4+\left(x+3\right)^4=2m\left(1\right)\)
Đặt \(x+2=t\)
Khi đó phương trình \(\left(1\right)\) trở thành \(\left(t-1\right)^4+\left(t+1\right)^4=2m\)
\(\Leftrightarrow2t^4+12t^2-2m+2=0\)
\(\Leftrightarrow t^4+6t^2-m+1=0\left(2\right)\)
Đặt \(t^2=u\left(u\ge0\right)\)
Khi đó phương trình \(\left(2\right)\) trở thành \(u^2+6u-m+1=0\left(3\right)\)
Thay \(m=1\) vào \(\left(3\right)\) ta có:
\(u^2+6u-1+1=0\Leftrightarrow u^2+6u=0\Leftrightarrow u\left(u+6\right)=0\Leftrightarrow\left[{}\begin{matrix}u=0\\u+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}u=0\left(\text{nhận}\right)\\y=-6\left(\text{loại}\right)\end{matrix}\right.\)
\(\Rightarrow x+2=0\Leftrightarrow x=-2\)
Vậy với \(m=1\) thì phương trình có nghiệm là \(x=-2\).
b) Để phương trình có hai nghiệm phân biệt thì \(\left(3\right)\) trái dấu \(\Leftrightarrow-m+1< 0\Leftrightarrow m>1\)
Vậy với \(m>1\) thì phương trình có hai nghiệm phân biệt.

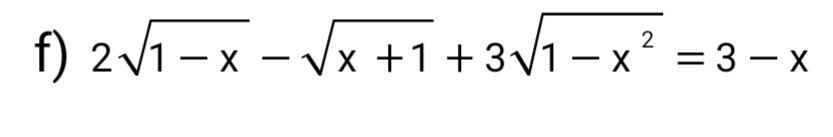 Giải pt . Mn giúp mik vs
Giải pt . Mn giúp mik vs


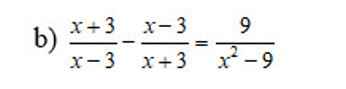
co phai toan lop 9 khong z ._.