Chứng minh rằng : a) S \(\le\frac{a^2+b^2}{4}\)với S là diện tích của tam giác có độ dài hai cạnh bằng a , b .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


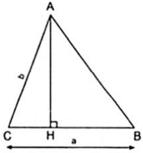
Xét tam giác ABC có BC = a, AC = b
Kẻ AH ⊥ BC thì AH và AC lần lượt là đường xiên.
Đường vuông góc kẻ từ A ở ngoài đường thẳng BC đến đường thẳng đó nên đường AH là đường ngắn nhất hay AH ≤ AC.
Khi đó ta có: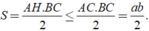
Mặt khác ta có:
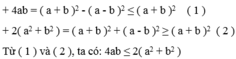
⇒ 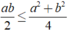
hay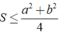 (đpcm)
(đpcm)


BĐT trên bị ngược dấu rồi.
Theo công thức Heron:
\(S=\dfrac{1}{4}\sqrt{\left(a+b+c\right)\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)}\).
Do đó ta chỉ cần cm:
\(\left(a+b+c\right)\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)\leq a^2b^2+b^2c^2+c^2a^2\). (1)
Ta có \(\left(1\right)\Leftrightarrow a^4+b^4+c^4-a^2b^2-b^2c^2-c^2a^2\ge0\Leftrightarrow\dfrac{\left(a^2-b^2\right)^2}{2}+\dfrac{\left(b^2-c^2\right)^2}{2}+\dfrac{\left(c^2-a^2\right)^2}{2}\ge0\) (luôn đúng).
Do đó bđt ban đầu cũng đúng.
Đẳng thức xảy ra khi tam giác đó đều.

Gọi chiều cao tương ứng với các cạnh a, b, c là ha ; hb ; hc
Ta có \(S=\frac{1}{2}a.h_a=\frac{1}{2}b.h_b=\frac{1}{2}c.h_c\)
Theo quan hệ giữa đường vuông góc và đường xiên thì \(h_a\le b;h_b\le c;h_c\le a\)
Vậy nên \(S=\frac{1}{2}a.h_a\le\frac{1}{2}a.b\Rightarrow2S\le ab\)
Tương tự \(2S< bc;2S< ca\)

Vẽ AH _|_ CD: \(S_{ACD}=\frac{1}{2}ah\le\frac{1}{2}ab\)
\(\Rightarrow4S_{ACD}\le2ab\le a^2+b^2\) (Theo BĐT Cosi)
Tương tự \(4S_{ABC}\le c^2+d^2\)
Vậy \(4\left(S_{ACD}+S_{ABC}\right)\le a^2+b^2+c^2+d^2\) hay \(S\le\frac{a^2+b^2+c^2+d^2}{4}\)
Dấu "=" xảy ra <=> \(\Delta\)ABC vuông ở B và \(\Delta\)ADC vuông ở D
=> ABCD là hình vuông
S = a.b/2
Xét : a^2+b^2/4 - ab/2 = a^2+b^2-2ab/4 = (a-b)^2/4 >= 0
=> ab/2 < = a^2+b^2/4
=> S < = a^2+b^2/4
=> đpcm
Tk mk nha
Bạn dưới Nguyễn Anh Quân nhầm rồi ; đây là tam giác thường chứ ko phải tam giác vuông