Cho tam giác ABC = tam giác GIK, biết IG:IK:KG=2:3:4
Chu vi tam giác GIK = 36 . Tính các cạnh tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

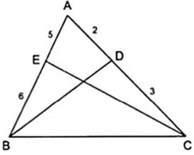
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
+ AB/BC = AD/DC = 2/3 = 4/6
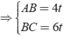 với t > 0
với t > 0
+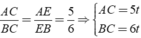
Theo giả thiết ta có: P A B C = A B + A C + B C = 15 t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )

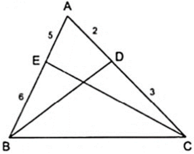
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
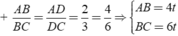 với t > 0
với t > 0
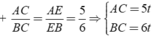
Theo giả thiết ta có: PABC = AB + AC + BC = 15t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )

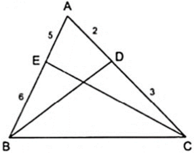
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
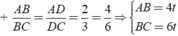 với t > 0
với t > 0
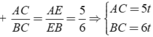
Theo giả thiết ta có: PABC = AB + AC + BC = 15t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )

AB/MN=BC/NP=CA/PM=(AB+BC+CA)/(MN+NP+PM)=(2+3+4)/36=1/4
=> AB/MN=2/MN=1/4=> MN=8
Tương tự tính ra NP và PM
Tính chu vi của tam giác ABC là:9cm
Lấy chu vi tam giác MNP/tam giác ABC là: 36/9=4cm
=>MN=4.2=8(cm)
NP=4.3=12(cm)
MP=4.4=16(cm)

6.)
Khi 2 tam giác đồng dạng với nhau thì cạnh nhỏ nhất của tam giác này sẽ tương ứng với cạnh nhỏ nhất của tam giác kia.
Theo đề:\(A'B'\)=4,5
Ta có:\(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
\(\Rightarrow\)\(\frac{4,5}{3}=\frac{B'C'}{5}=\frac{C'A'}{7}\)
\(\Rightarrow\)\(B'C'=7,5cm,C'A'=10,5cm\)

Đặt AB=a; AC=b
Theo đề, ta có: a/3=b/4
Đặt a/3=b/4=k
=>a=3k; b=4k
Theo đề, ta có: 3k+4k+5k=36
=>12k=36
=>k=3
=>AB=9; AC=12; BC=15
Ta có:
IG/2 = IK/3 = KG/4 và IG + IK + KG = 36
Áp dụng tính chất của dãy tỉ số bằng nhau, có:
\(\frac{IG}{2}=\frac{IK}{3}=\frac{KG}{4}=\frac{IG+IK+KG}{2+3+4}=\frac{36}{9}=4\)
Suy ra: \(\frac{IG}{2}=4\Rightarrow IG=4\cdot2=8\)
\(\frac{IK}{4}=4\Rightarrow IK=4\cdot4=16\)
\(\frac{KG}{4}=4\Rightarrow KG=4\cdot4=16\)
Mà tam giác ABC = tam giác GIK
=> AB = IG; BC = IK; AC = KG (các cặp cạnh tương ứng)
=> AB = IG = 8; BC = IK = 16; AC = KG = 16
Áp dụng t/c của dãy tỉ số = nhau nha bạn ^^