Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Tiếp tuyến tại A và B của (O) cắt nhau tại C.CM cắt (I) tại N'
Xét \(\Delta CAM\) và \(\Delta CN'A:\) Ta có: \(\left\{{}\begin{matrix}\angle ACN'chung\\\angle CAM=\angle CN'A\end{matrix}\right.\)
\(\Rightarrow\Delta CAM\sim\Delta CN'A\left(g-g\right)\Rightarrow\dfrac{CA}{CN'}=\dfrac{CM}{CA}\Rightarrow CA^2=CM.CN'\)
mà \(CA^2=CB^2\Rightarrow CB^2=CM.CN'\Rightarrow\dfrac{CB}{CM}=\dfrac{CN'}{CB}\)
Xét \(\Delta CBM\) và \(\Delta CN'B:\) Ta có: \(\left\{{}\begin{matrix}\angle BCN'chung\\\dfrac{CB}{CM}=\dfrac{CN'}{CB}\end{matrix}\right.\)
\(\Rightarrow\Delta CBM\sim\Delta CN'B\left(c-g-c\right)\Rightarrow\angle CBB=\angle CN'B\Rightarrow N'\in\left(J\right)\)
\(\Rightarrow N\equiv N'\Rightarrow MN\) luôn đi qua điểm C mà A,B cố định
\(\Rightarrow C\) cố định \(\Rightarrow\) đpcm
b) mình chỉ chứng minh được N thuộc 1 đường tròn cố định thôi,còn chạy trên đoạn thẳng hình như là ko được
Ta có: \(\angle ANB=\angle ANM+\angle BNM=\dfrac{1}{2}\angle AIM+\dfrac{1}{2}\angle BJM\)
Xét \(\Delta AIM\) và \(\Delta AOB:\) Ta có: \(\left\{{}\begin{matrix}\angle OABchung\\\dfrac{IA}{OA}=\dfrac{IM}{OB}\end{matrix}\right.\)
\(\Rightarrow\Delta AIM\sim\Delta AOB\left(c-g-c\right)\Rightarrow\angle AIM=\angle AOB\)
Tương tự \(\Rightarrow\angle BJM=\angle AOB\)
\(\Rightarrow\angle ANB=\dfrac{1}{2}\angle AOB+\dfrac{1}{2}\angle AOB=\angle AOB\)
\(\Rightarrow N\in\left(AOB\right)\) mà A,O,B cố định \(\Rightarrow N\in\left(AOB\right)\) cố định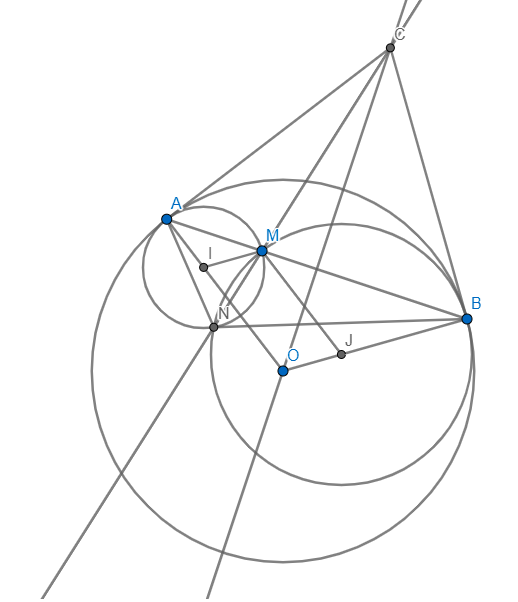
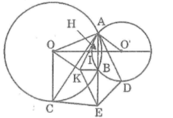
Vì AB ⊥ KB nên AE ⊥ KB
Lại có: AB = BE (tính chất đối xứng tâm)
Suy ra: KA = KE (tính chất đường trung trực) (3)
Ta có: IO = IO’ (gt)
IA = IK (chứng minh trên)
Tứ giác AOKO’ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: OK // O’A và OA // O’K
CA ⊥ O’A (vì CA là tiếp tuyến của đường tròn (O’))
OK // O’A (chứng minh trên)
Suy ra: OK ⊥ AC
Khi đó OK là đường trung trực của AC
Suy ra: KA = KC (tính chất đường trung trực) (4)
DA ⊥ OA (vì DA là tiếp tuyến của đường tròn (O))
O’K // OA (chứng minh trên)
Suy ra: O’K ⊥ DA
Khi đó O’K là đường trung trực của AD
Suy ra: KA = KD (tính chất đường trung trực) (5)
Từ (3), (4) và (5) suy ra: KA = KC = KE = KD
Vậy bốn điểm A, C, E, D cùng nằm trên một đường tròn.3
ke tiep tuyen chung tai A