tìm MIN : x2 -7x+2
MAX : x2 -12x + 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



y = −2 x 2 + 7x − 5. TXĐ: R
y′ = −4x + 7, y′ = 0 ⇔ x = 7/4
y′′ = −4 ⇒ y′′(7/4) = −4 < 0
Vậy x = 7/4 là điểm cực đại của hàm số và y CD = 9/8

Từ đề bài suy ra: 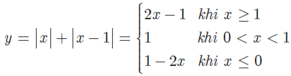
Bảng biến thiên
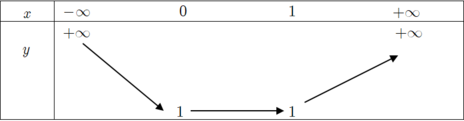
Ta có y(-2) =5; y(2) =3
Dựa vào bảng biến thiên ta có

Chọn D.

Đáp án D
Ta có lim x → 2 − f x = lim x → 2 − 2 x 2 − 7 x + 6 x − 2 = lim x → 2 − 2 x 2 − 7 x + 6 x − 2 = lim x → 2 − − 2 x − 3 = − 1
Và lim x → 2 − f x = lim x → 2 − a + 1 − x 2 + x = a − 1 4 ; f 2 = a − 1 4 .
Theo bài ra, ta có lim x → 2 + f x = lim x → 2 − f x = f 2 ⇒ a = − 3 4
Do đó, bất phương trình − x 2 + a x + 7 4 > 0 ⇔ − x 2 − 3 4 x + 7 4 > 0 ⇔ − 7 4 < x < 1.

Không có max
`a)sqrt{x^2-2x+5}`
`=sqrt{x^2-2x+1+4}`
`=sqrt{(x-1)^2+4}`
Vì `(x-1)^2>=0`
`=>(x-1)^2+4>=4`
`=>sqrt{(x-1)^2+4}>=sqrt4=2`
Dấu "=" xảy ra khi `x=1.`
`b)2+sqrt{x^2-4x+5}`
`=2+sqrt{x^2-4x+4+1}`
`=2+sqrt{(x-2)^2+1}`
Vì `(x-2)^2>=0`
`=>(x-2)^2+1>=1`
`=>sqrt{(x-2)^2+1}>=1`
`=>sqrt{(x-2)^2+1}+2>=3`
Dấu "=" xảy ra khi `x=2`

*) Hàm số y = -x² có a = -1 < 0
Do đó hàm số đồng biến khi x < 0 và nghịch biến khi x > 0
*) Hàm số y = 4x² có a = 4 > 0
Do đó hàm số đồng biến khi x > 0 và nghịch biến khi x < 0
\(x^2-7x+2=x^2-2\cdot x\cdot\dfrac{7}{2}+\dfrac{49}{4}-\dfrac{41}{4}\)
\(=\left(x-\dfrac{7}{2}\right)^2-\dfrac{41}{4}>=-\dfrac{41}{4}\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{7}{2}=0\)
=>\(x=\dfrac{7}{2}\)
\(x^2-12x+5\)
\(=x^2-12x+36-31=\left(x-6\right)^2-31>=-31\forall x\)
Dấu '=' xảy ra khi x-6=0
=>x=6
`x^2 - 7x + 2`
`= x^2 - 2.x . 7/2 + (7/2)^2 - 41/4`
`= (x - 7/2)^2 - 41/4`
Do `(x - 7/2)^2 >= 0=> (x - 7/2)^2 - 41/4 >= - 41/4`
Dấu = xảy ra khi:
`x - 7/2 = 0`
`<=> x = 7/2`
Vậy ...
-----------------------
`x^2 - 12x + 5`
`= x^2 - 2.x.6 + 6^2 - 31`
`= (x-6)^2 - 31`
Do `(x-6)^2 >= 0 => (x-6)^2 - 31>= -31`
Dấu = có khi:
`x - 6 = 0`
`<=> x = 6`
Vậy .... (không có max )