Câu 1. Chứng minh √7 là số vô tỉ.
Câu 2.
a) Chứng minh: (ac + bd)2 + (ad – bc)2 = (a2 + b2)(c2 + d2)
b) Chứng minh bất dẳng thức Bunhiacôpxki: (ac + bd)2 ≤ (a2 + b2)(c2 + d2)
Câu 3. Cho x + y = 2. Tìm giá trị nhỏ nhất của biểu thức: S = x2 + y2.
Câu 4.
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy:
b) Cho a, b, c > 0. Chứng minh rằng:
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
Câu 5. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức: M = a3 + b3.
Câu 6. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức: N = a + b.
Câu 7. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 8. Tìm liên hệ giữa các số a và b biết rằng: |a + b| > |a - b|
Câu 9.
a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8
Câu 10. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
Câu 11. Tìm các giá trị của x sao cho:
a) |2x – 3| = |1 – x|
b) x2 – 4x ≤ 5
c) 2x(2x – 1) ≤ 2x – 1.
Câu 12. Tìm các số a, b, c, d biết rằng: a2 + b2 + c2 + d2 = a(b + c + d)
Câu 13. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Câu 14. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.
Câu 15. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau:
x2 + 4y2 + z2 – 2a + 8y – 6z + 15 = 0
Câu 16. Tìm giá trị lớn nhất của biểu thức:
Câu 17. So sánh các số thực sau (không dùng máy tính):
Câu 18. Hãy viết một số hữu tỉ và một số vô tỉ lớn hơn √2 nhưng nhỏ hơn √3
Câu 19. Giải phương trình: .
Câu 20. Tìm giá trị lớn nhất của biểu thức A = x2y với các điều kiện x, y > 0 và 2x + xy = 4.
Câu 21. Cho .
Hãy so sánh S và .
Câu 22. Chứng minh rằng: Nếu số tự nhiên a không phải là số chính phương thì √a là số vô tỉ.
Câu 23. Cho các số x và y cùng dấu. Chứng minh rằng:
Câu 24. Chứng minh rằng các số sau là số vô tỉ:
Câu 25. Có hai số vô tỉ dương nào mà tổng là số hữu tỉ không?
Câu 26. Cho các số x và y khác 0. Chứng minh rằng:
Câu 27. Cho các số x, y, z dương. Chứng minh rằng:
Câu 28. Chứng minh rằng tổng của một số hữu tỉ với một số vô tỉ là một số vô tỉ.
Câu 29. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.
Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].
Câu 32. Tìm giá trị lớn nhất của biểu thức:
Câu 33. Tìm giá trị nhỏ nhất của: với x, y, z > 0.
Câu 34. Tìm giá trị nhỏ nhất của: A = x2 + y2 biết x + y = 4.
Câu 35. Tìm giá trị lớn nhất của: A = xyz(x + y)(y + z)(z + x) với x, y, z ≥ 0; x + y + z = 1.
Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:
a) ab và a/b là số vô tỉ.
b) a + b và a/b là số hữu tỉ (a + b ≠ 0)
c) a + b, a2 và b2 là số hữu tỉ (a + b ≠ 0)
Câu 37. Cho a, b, c > 0. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 38. Cho a, b, c, d > 0. Chứng minh:
Câu 39. Chứng minh rằng [2x] bằng 2[x] hoặc 2[x] + 1
Câu 40. Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Câu 41. Tìm các giá trị của x để các biểu thức sau có nghĩa:
Câu 42.
a) Chứng minh rằng: | A + B | ≤ | A | + | B |. Dấu “ = ” xảy ra khi nào?
b) Tìm giá trị nhỏ nhất của biểu thức sau: .
c) Giải phương trình:
Câu 43. Giải phương trình: .
Câu 44. Tìm các giá trị của x để các biểu thức sau có nghĩa:


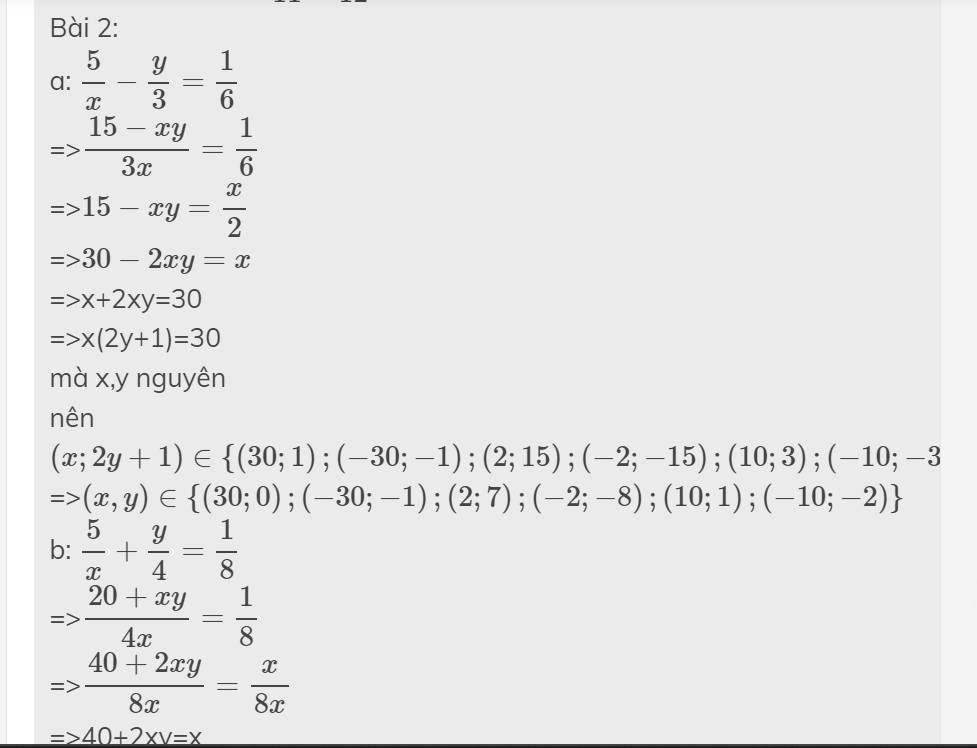

Câu 2:
35 + y x 12 = 83
y x 12 = 83 - 35
y x 12 = 48
y = 48 : 12
y = 4
27 x ( y : 34) = 40,5
(y : 34) = 40,5 : 27
y : 34 = 1,5
y = 1,5 x 34
y = 51
Câu 3:
Khi trừ cả tử và mẫu cho cùng một số tự nhiên thì hiệu của mẫu số và tử số không đổi và bằng:
27 - 17 = 10
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Tử số mới là:
10 : (2 -1) = 10
Vậy để được phân số có giá trị bằng \(\dfrac{1}{2}\)cần cùng trừ ở tử số và mẫu số ban đầu số tự nhiên là:
17 - 10 = 7
Đáp số: 7