Cho tam giác cân $ABC$, có $BA=BC=a$, $AC=b$. Đường phân giác của góc $A$ cắt $BC$ tại $M$, đường phân giác góc $C$ cắt $BA$ tại $N$.
a. Chứng minh $MN$ // $AC$.
b. Tính $MN$ theo $a$, $b$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 2 2017
Ta có: 
(chứng minh trên)
Suy ra:
Hay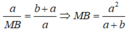 
Trong ΔBAC, ta có:
MN //AC (chứng minh trên)
Và 
Vậy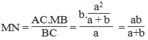 
CM
31 tháng 12 2018
Trong △ BAC, ta có: AM là đường phân giác của (BAC)
Suy ra: 
(tỉnh chất đường phân giác) (1)
CN là đường phân giác của (BCA)
Suy ra: 
(tỉnh chất đường phân giác) (2)
Lại có: AB = CB = a (gt)
Từ (1), (2) và (gt) suy ra: 
Trong
△
BAC, ta có: 
Suy ra: MN // AC (theo định lí đảo của định lí Ta-lét).
S
6 tháng 3 2020
Hình bạn tự vẽ nhé!
tg ABC cân tại B vì có BA=BC
=> góc BAC= (180-gB)/2
Tam giác ANC và CMA bằng nhau theo TH g-c-g vì có chung AC,gBAC=gBCA, gMAC=gNCA ( bằng 1 nửa góc lớn)
=> AN=MC
=>AB-AN=BC-MC
=>NB=MB
=>tgBMN cân tại B
=> gBNM= (180-gB)/2 và bằng góc BAC
=> MN//AC ( có 2 góc đồng vị=nhau)
b, Theo tính chất tia phân giác của góc BCA, vì CN là phân giác=> BN/AN=BC/AC ( nếu ko nhớ thì mở lại sách nhé!)
=>BN/(BN+AN)=BC/(BC+AC) ( theo tc tỉ lệ thức nhé)
=>BN/BA=8/14
Xét tg ABC có MN//AC => BN/AN=MN/AC=> 8/14=MN/6 => MN=8.6/14=3,43...( sao lẻ thế nhỉ)
Xem đúng không nhé
a: Xét ΔBAC có AM là phân giác
nên \(\dfrac{BM}{MC}=\dfrac{AB}{AC}\)
=>\(\dfrac{BM}{MC}=\dfrac{a}{b}\)
=>\(\dfrac{BM}{a}=\dfrac{MC}{b}\)
mà BM+MC=BC=a
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BM}{a}=\dfrac{MC}{b}=\dfrac{BM+MC}{a+b}=\dfrac{a}{a+b}\)
=>\(BM=\dfrac{a\cdot a}{a+b}=\dfrac{a^2}{a+b}\)
Xét ΔBCA có CN là phân giác
nên \(\dfrac{BN}{NA}=\dfrac{BC}{CA}\)
=>\(\dfrac{BN}{NA}=\dfrac{a}{b}\)
=>\(\dfrac{BN}{NA}=\dfrac{BM}{MC}\)
Xét ΔBAC có \(\dfrac{BN}{NA}=\dfrac{BM}{MC}\)
nên MN//AC
b: Xét ΔBAC có MN//AC
nên \(\dfrac{MN}{AC}=\dfrac{BM}{BC}\)
=>\(\dfrac{MN}{b}=\dfrac{a^2}{a+b}:a=\dfrac{a}{a+b}\)
=>\(MN=\dfrac{a\cdot b}{a+b}\)