Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét \(\Delta ABM\)và \(\Delta CBN\)có :
\(\widehat{B}\)là góc chung
\(\frac{AB}{BC}=\frac{NB}{MB}\)( Do tam giác ABC cân tại B , \(AB=BC\) và \(\widehat{A}=\widehat{C}\))
\(\Rightarrow\Delta ABM\)\(\infty\)\(\Delta CBN\)\(\left(c.g.c\right)\)
b) do \(\Delta ABM\infty\Delta BCN\left(c.g.c\right)\)(chứng minh câu a)
ta có tỉ lệ : \(\frac{BM}{BC}=\frac{BN}{AB}\)=MN/AC(dpcm)
c) bạn tự làm nka câu này dễ

Ta có: ![]() (chứng minh trên)
(chứng minh trên)
Suy ra:![]()
Hay 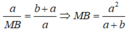
Trong ΔBAC, ta có:
MN //AC (chứng minh trên)
Và ![]()
Vậy 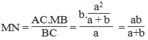

a)Xét tam giác ABM và tam giác BCN có:
+AB=CB(Theo D/lí tam giác cân)
+Góc B chung
+AM=CN(Vì là hai cạnh tương ứng của hai tam giác bằng nhau)
=> Tam giác ABM=BCN(theo t.hợp C.G.C)\
Vậy tam giác ABM=tam giác BCN