Rút gọn phân thức\(\dfrac{1-x^2}{x\left(x-1\right)}\)với x\(\ne\)0,với x\(\ne\)1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : \(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{1}{x+\sqrt{x}}\right)\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right)\)
\(=\left(\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\left(\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right)\)
\(=\left(\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\left(\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right)\)
\(=\left(\dfrac{\sqrt{x}-1}{\sqrt{x}}\right)\left(\dfrac{1}{\sqrt{x}-1}\right)=\dfrac{1}{\sqrt{x}}\)
B = \(\left[\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right].\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right)\)
= \(\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{1}{\sqrt{x}}\)

Sửa đề: \(A=\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right):\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
Ta có: \(A=\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right):\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
\(=\left(\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}\right):\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
\(=\dfrac{x+\sqrt{x}-2-x+\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{2}{x-1}\)

a) \(\sqrt{\dfrac{x-2\sqrt{x}+1}{x+2\sqrt{x}+1}}\sqrt{\dfrac{\left(\sqrt{x+1}\right)^2}{\left(\sqrt{x}+1\right)^2}}\)
=\(\dfrac{\sqrt{x}-1}{\sqrt{x}+1};x\ge0\)
b) Ta có: \(\dfrac{x-1}{\sqrt{y}-1}\cdot\sqrt{\dfrac{\left(y-2\sqrt{y}+1\right)^2}{\left(x-1\right)^4}}\)
\(=\dfrac{x-1}{\sqrt{y}-1}\cdot\dfrac{\sqrt{y}-1}{\left(x-1\right)^2}\)
\(=\dfrac{1}{x-1}\)

Lời giải:
\(P=\left[\frac{\sqrt{x}+1}{(\sqrt{x}+1)(\sqrt{x}-1)}+\frac{x}{\sqrt{x}(\sqrt{x}-1)}\right]:\frac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\left[\frac{1}{\sqrt{x}-1}+\frac{\sqrt{x}}{\sqrt{x}-1}\right].\frac{\sqrt{x}}{\sqrt{x}+1}\)
\(=\frac{\sqrt{x}+1}{\sqrt{x}-1}.\frac{\sqrt{x}}{\sqrt{x}+1}=\frac{\sqrt{x}}{\sqrt{x}-1}\)
b. Áp dụng BĐT AM-GM
\(M=P\sqrt{x}=\frac{x}{\sqrt{x}-1}=\frac{x-1+1}{\sqrt{x}-1}=\sqrt{x}+1+\frac{1}{\sqrt{x}-1}\)
\(=(\sqrt{x}-1)+\frac{1}{\sqrt{x}-1}+2\geq 2\sqrt{(\sqrt{x}-1).\frac{1}{\sqrt{x}-1}}+2=2+2=4\)
Vậy $M_{\min}=4$ khi $\sqrt{x}-1=\frac{1}{\sqrt{x}-1}$
$\Rightarrow \sqrt{x}-1=0$
$\Leftrightarrow x=1$

a) \(P=\dfrac{1}{2-\sqrt{3}}+\dfrac{1}{2+\sqrt{3}}\)
\(=\dfrac{2+\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}+\dfrac{2-\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\)
\(=\dfrac{2+\sqrt{3}+2-\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\)
\(=\dfrac{4}{4-3}\)
\(=4\)
b) \(Q=\left(1+\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\right).\dfrac{1}{\sqrt{x}}vớix>0,x\ne4\)
\(=\left(\dfrac{\sqrt{x}-2+\sqrt{x}+2}{\sqrt{x}-2}\right).\dfrac{1}{\sqrt{x}}\)
\(=\)\(\dfrac{2\sqrt{x}}{\sqrt{x}-2}.\dfrac{1}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2}{\sqrt{x}-2}\)

a, \(A=\dfrac{4\left(3-\sqrt{7}\right)}{2}+2\sqrt{7}=\dfrac{12}{2}=6\)
b, \(B=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2}{\sqrt{x}}\right):\dfrac{2-\sqrt{x}}{x-1}\)
\(=\left(\dfrac{\sqrt{x}-2\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\dfrac{2-\sqrt{x}}{x-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
nhờ bạn làm rõ vì sao \(\dfrac{\sqrt{x}-2\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{2-\sqrt{x}}{x-1}\) lại bằng \(\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
mình xin cảm ơn

\(=>P=\left[\dfrac{\sqrt{x}.\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\left[\dfrac{\sqrt{x}-1+2}{x-1}\right]\)
\(P=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{x-1}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}}:\dfrac{1}{\sqrt{x}-1}=\dfrac{x-1}{\sqrt{x}}\)
Ta có: \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}+1}\)
\(=\dfrac{x-1}{\sqrt{x}}\)
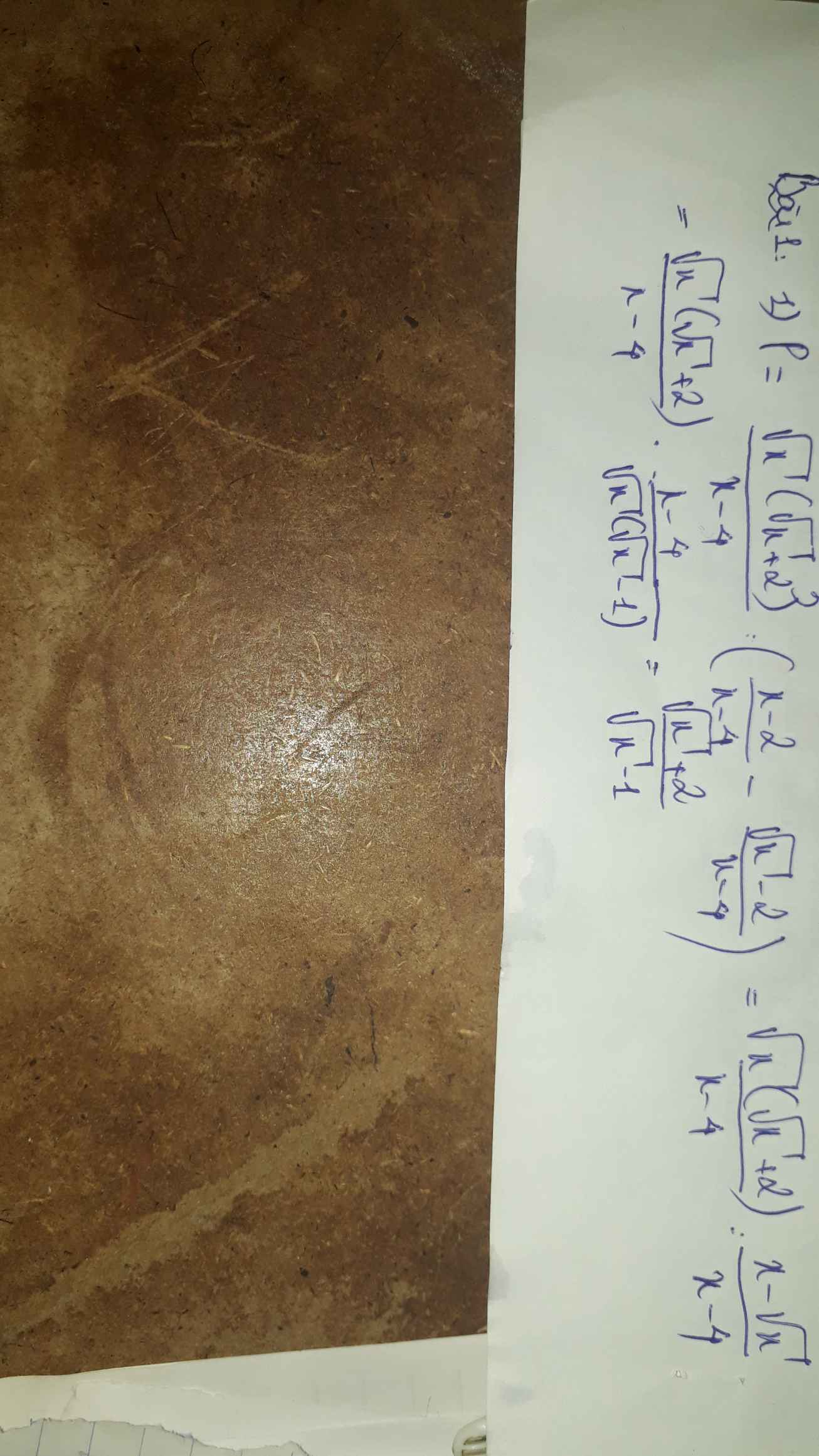



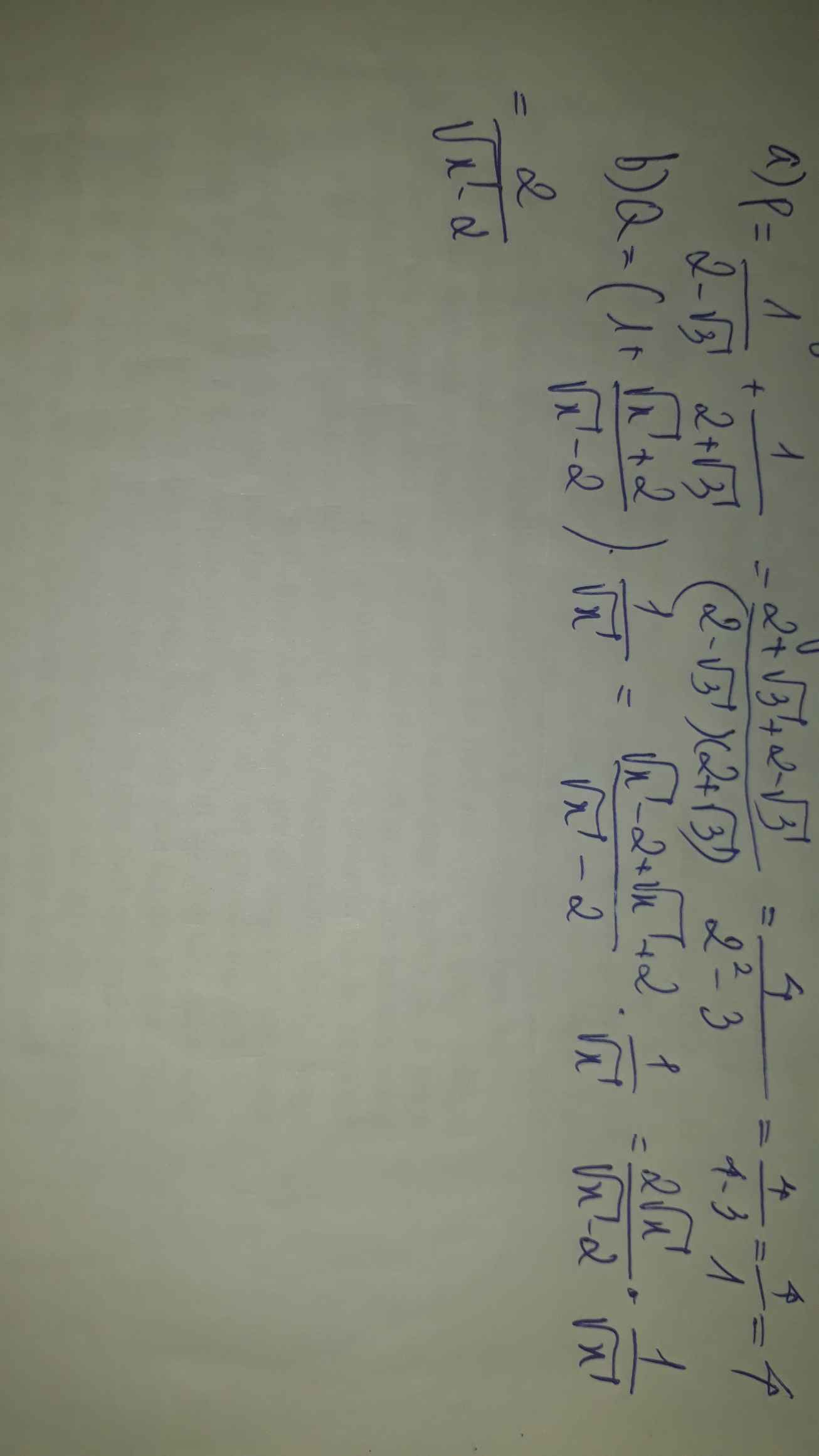
Với x ≠ 0; x ≠ 1, ta có:
(1 - x²)/[x(x - 1)]
= -(x - 1)(x + 1)/[x(x - 1)]
= -(x + 1)/x