cho tam giác ABC cân tại A,đường trung tuyến AH .Gọi I,K lần lượt là trung điểm của AC và AB lấy điểm E sao cho I là trung điểm của HE a. CMR AHCE là HCN, HBAE là HBH b. CMR AKHI là hình thoi c.tam giác ABC cần thêm điều kiện gì để AHCE là h vuôngcho xin giải chi tiết ah , gấp lắm r...
Đọc tiếp
cho tam giác ABC cân tại A,đường trung tuyến AH .Gọi I,K lần lượt là trung điểm của AC và AB lấy điểm E sao cho I là trung điểm của HE a. CMR AHCE là HCN, HBAE là HBH b. CMR AKHI là hình thoi c.tam giác ABC cần thêm điều kiện gì để AHCE là h vuông
cho xin giải chi tiết ah , gấp lắm r đấy
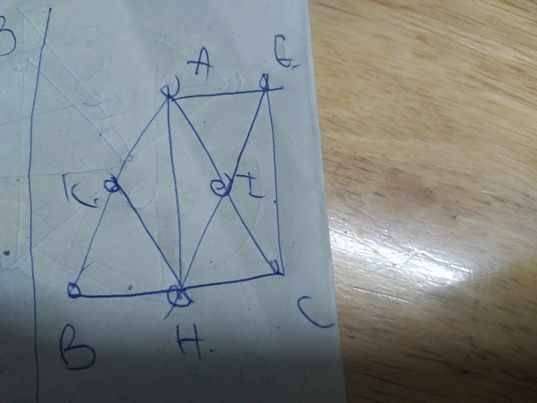
a: Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là phân giác của góc BAC và AH\(\perp\)BC
Xét tứ giác AHCE có
I là trung điểm chung của AC và HE
=>AHCE là hình bình hành
Hình bình hành AHCE có \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật
=>AE//CH và AE=CH
Ta có: AE//CH
H\(\in\)BC
Do đó: AE//HB
Ta có: AE=CH
CH=HB
Do đó: AE=HB
Xét tứ giác AEHB có
AE//HB
AE=HB
Do đó: AEHB là hình bình hành
c: Xét ΔABC có
H,I lần lượt là trung điểm của CB,CA
=>HI là đường trung bình của ΔABC
=>HI//AB và HI=AB/2
Ta có: HI//AB
K\(\in\)AB
Do đó: HI//AK
Ta có: HI=AB/2
AK=KB=AB/2
Do đó: HI=AK=KB
Xét tứ giác AKHI có
HI//AK
HI=AK
Do đó: AKHI là hình bình hành
Hình bình hành AKHI có AH là phân giác của góc KAI
nên AKHI là hình thoi
c: Để hình chữ nhật AHCE trở thành hình vuông thì AH=CH
mà \(CH=\dfrac{CB}{2}\)
nên \(AH=\dfrac{CB}{2}\)
Xét ΔABC có
AH là đường trung tuyến
\(AH=\dfrac{CB}{2}\)
Do đó: ΔABC vuông tại A
=>\(\widehat{BAC}=90^0\)