Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

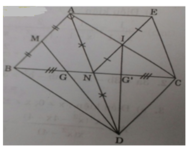
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)

Bạn tự vẽ hình nha :))
a) Xét tứ giác ABCD có :
NB = NC ( N là trung điểm của BC ( gt ))
NA = ND ( D đối xứng với A qua N ( gt ))
BC giao AD tại N
=> Tư giác ABCD là hình bình hành ( dhnb )
mà \(\widehat{BAC}=90^0\) ( \(\Delta ABC\)vuông tại A (gt))
=> Tứ giác ABCD là HCN ( dhnb )
b) Xét tam giác ABC có :
N là trung điểm của BC ( gt )
I là trung điểm của AC ( gt )
=> NI là đường trung bình của tam giác ABC ( đ/n )
=> NI // AB ( t/c )
=> \(\widehat{BAC}=\widehat{NIC}=90^0\) ( đồng vị )
=> NI \(\perp\)AC
Xét tứ giác ANCE có :
IA = IC ( I là trung điểm của AC (gt))
IN = IE ( E đối xứng N qua I (gt))
AC giao NE tại I
=> Tứ giác ANCE là hình bình hành ( dhnb )
mà NI \(\perp\)AC ( cmt )
=> Tứ giác ANCE là hình thoi ( dhnb )
c) Xét tam giác ABD có :
DM là đường trung tuyến
BN là đường trung tuyến
DM giao BN tại G
=> G là trọng tâm.
\(\Rightarrow BG=\frac{2}{3}BN\) mà \(BN=\frac{1}{2}BC\) ( ABCD là HCN (a))
\(\Rightarrow BG=\frac{1}{3}BC\)
CM tương tự, ta có : \(CH=\frac{1}{3}BC\)
\(\Rightarrow BG=CH\left(=\frac{1}{3}BC\right)\)

a: Xét tứ giác ABDC có
N là trung điểm của AD
N là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABDC là hình chữ nhật
b: Xét tứ giác ANCE có
I là trung điểm của AC
I là trung điểm của NE
Do đó: ANCE là hìnhbình hành
mà NA=NC
nen ANCE là hình thoi

tui chỉ làm phần d thôi nha, mấy câu trên cậu tự chứng minh nhé
Hình tự vẽ
Lấy M là trung điểm của CK
mà có I là tđ của HK
suy ra MI là đường trung bình tam giác HKC và MI song song với CH
mà CH lại vuông góc với HF ( tự c/m) nên MI vuông góc với HF
Xét tam giác HFM có I là trực tâm ( tự ghi rõ ) suy ra FI vuông góc với HM mà có
M là tđ CK, H là tđ BC ( tự c/m) suy ra đường trung bình nên HM song song với BK suy ra đpcm
tui chỉ ghi qua thui, cậu tự trình bày rõ ràng nhé
mấy cái tự c/m ko dài đâu, đều hiện lên trên hình cậu vẽ rùi, đều có sẵn chỉ cần vài dòng thui, đừng lười, THI TỐT NHẾ
MAI TUI THI TOÁN VỚI ANH ĐÓ, THANKS VÌ ĐỀ BÀI RẤT HAY NHA.

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE