x.y = -20 và x<y
giúp mình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 12 2014
a, Do UCLN là 5 nên a, b chia hết cho 5 => tận cùng là 0 hoặc 5
Ta có 20 = 15 + 5 = 18 + 2=19+1=17+3=16+4=14+6=13+7=12+8=11+9
=> 2 số a và b là 15 và 5 hoặc 5 và 15
Bài sau làm tương tự em nhé :)
TC
27 tháng 1 2023
đặt `x/4 =y/5 =k`
`=>{(x=4k),(y=5k):}`
ta có
`x/4 =y/5 = (x*y)/(5*4) = 20/20 =1 =k^2`
`=> k = +-1`
`=>`\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x=4\cdot1=4\\x=4\cdot\left(-1\right)=-4\end{matrix}\right.\\\left[{}\begin{matrix}y=1\cdot5=5\\y=-1\cdot5=-5\end{matrix}\right.\end{matrix}\right.\)
PN
3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 12 2023
a; \(x\); y \(\in\) Z
20 = 22.5
Ư(20) = {-20; -10; -5; -4; -2; -1; 1; 2; 4; 5; 10; 20}
Lập bảng ta có:
| \(x\) | -20 | -10 | -5 | -4 | -2 | -1 | 1 | 2 | 4 | 5 | 10 | 20 |
| y | -1 | -2 | -4 | -5 | -10 | -20 | 20 | 10 | 5 | 4 | 2 | 1 |
Vì \(x\) < y nên (\(x;y\)) = (-20; -1); (-10; -2); (-5; - 4); (1; 20); (4; 5)
HN
1
YN
19 tháng 9 2021
\(\frac{15}{x-9}=\frac{20}{y-12}=\frac{40}{z-24}\) và \(x.y=1200\) (Sửa đề)
Ta có:
\(\frac{x-9}{15}=\frac{y-12}{20}=\frac{z-24}{40}\Rightarrow\frac{x}{15}.\frac{9}{15}=\frac{y}{20}.\frac{12}{20}=\frac{z}{40}.\frac{24}{40}\)
Mà \(\frac{9}{15}=\frac{12}{20}=\frac{24}{40}=\frac{3}{5}\Rightarrow\frac{x}{15}=\frac{y}{20}=\frac{z}{40}\)
\(\Rightarrow\frac{x^2}{15^2}=\frac{y^2}{20^2}=\frac{z^2}{40^2}=\frac{x.y}{15.20}=\frac{1200}{300}=2^2\)
\(\Rightarrow x^2=2^2.15=\left(2.15\right)^2=30^2\Rightarrow x=\pm30\)
\(\Rightarrow y^2=2^2.20^2=\left(2.20\right)^2=40^2\Rightarrow y=\pm40\)
\(\Rightarrow z^2=2^2.40^2=\left(2.40\right)^2=80^2\Rightarrow z=\pm80\)
MT
0
L
1
PT
1
CM
28 tháng 10 2019
- Đặt (x; y) = d nên x = d.m; y = d.n với (m;n) =1. Giả sử x ≤ y thì m ≤ n.
- Ta có: x.y = dm.dn= d2.mn
BCNN(x; y) = x y x ; y = d 2 m . n d = d . m . n
- Ta có: BCNN (x;y) = 10 và x. y = 20 nên d = x y B C N N ( x ; y ) = 20 10 = 2
=> 2.m.n =10 nên m.n = 5
Bảng giá trị
PT
1
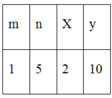
Lời giải:
** Bổ sung điều kiện $x,y$ là số nguyên
$xy=-20<0$ nên $x,y$ trái dấu. Mà $x< y$ nên $x<0; y>0$
Do đó, từ $xy=-20$ ta có các cặp $(x,y)$ thỏa mãn là:
$(-1,20), (-2,10), (-4,5), (-5,4), (-10,2), (-20,1)$