Một máy bay chở khách có khối lượng tổng cộng là 300 tấn. Lực đẩy tối đa của động cơ là 440 kN. Máy bay phải đạt tốc độ 285 km/h mới có thể cất cánh. Hãy tính chiều dài tối thiểu của đường băng để đảm bảo máy bay cất cánh được, bỏ qua ma sát giữa bánh xe của máy bay và mặt đường băng và lực cản không khí.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vật bắt đầu cất cánh có \(v_0=0\).
\(v=250km/h=\dfrac{625}{9}m/s\)
Gia tốc vật: \(a=\dfrac{v^2-v_0^2}{2S}=\dfrac{\left(\dfrac{625}{9}\right)^2-0}{2\cdot4000}=0,6m/s^2\)
Lực phát động của máy bay:
\(F=m\cdot a=500\cdot1000\cdot0,6=3\cdot10^5N\)

Áp dụng định luật II Niu-tơn cho chuyển động của máy bay :
F - F m s = ma ⇒ F - μ P = (P/g).( v 2 /2s)
với F là lực kéo của động cơ, F m s là lực ma sát với đường băng, a là gia tốc của máy bay khối lượng m trên đoạn đường băng dài s. Từ đó suy ra :
![]()
Như vậy, động cơ máy bay phải có công suất tối thiểu bằng:
P = Fv = 5,2. 10 3 .25. ≈ 130 kW

Đổi 297 km/h = 82,5 m/s
Gia tốc trung bình của máy bay trong quá trình bay là:
\(a = \frac{{{v_2} - {v_1}}}{{{t_2} - {t_1}}} = \frac{{82,5}}{{30}} = 2,75(m/{s^2})\)

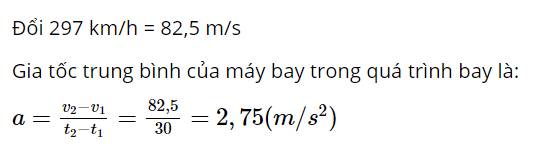

Ta có m = 300 tấn = 3.105 kg; F = 440 kN = 4,4.105 N; v = 285 km/h = 475/6 m/s
Gia tốc của máy bay là: \(a = \frac{F}{m} = \frac{{4,{{4.10}^5}}}{{{{3.10}^5}}} = \frac{{22}}{{15}}(m/{s^2})\)
Chiều dài tối thiểu của đường băng để đảm bảo máy bay cất cánh được là:
\(s = \frac{{{v^2} - v_0^2}}{{2.a}} = \frac{{{{\left( {\frac{{475}}{6}} \right)}^2}}}{{2.\frac{{22}}{{15}}}} \approx 2136,6(m)\)