Mọi người giúp mình bài này với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)

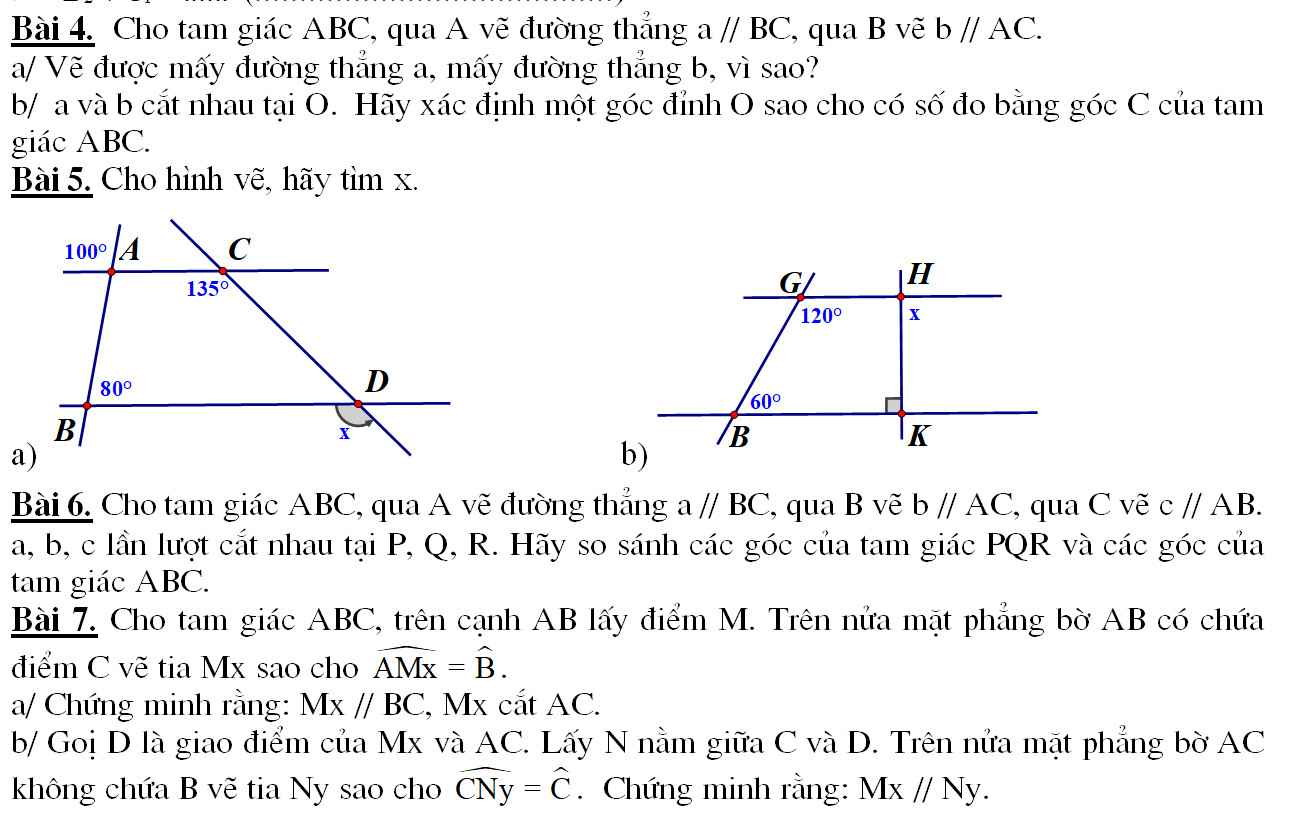
Bài 5:
A 1 2 3 4 B 1 C 1 D 1
Ta có : \(\widehat{A_1}+\widehat{A_3}=180^o\) (kề bù)
\(100^o+\widehat{A_3}=180^o\)
\(\widehat{A_3}=80^o\)
Ta có: \(\widehat{A_3}=\widehat{B_1}=80^o\)
\(\widehat{A_3}\) và \(\widehat{B_1}\) ở vị trí đồng vị
\(\Rightarrow AC//BD\)
\(\Rightarrow\widehat{C}_1=\widehat{D_1}=135^o\) (đồng vị)
\(x=135^o\)
b)
G H B K 1 1 1 1
Ta có: \(\widehat{G_1}+\widehat{B_1}=180^o\left(120^o+60^o=180^o\right)\)
\(\widehat{G_1}\) và \(\widehat{B_1}\) ở vị trí trong cùng phía
\(\Rightarrow QH//BK\)
\(\Rightarrow\widehat{H_1}=\widehat{K_1}=90^o\)(so le)
\(x=90^o\)

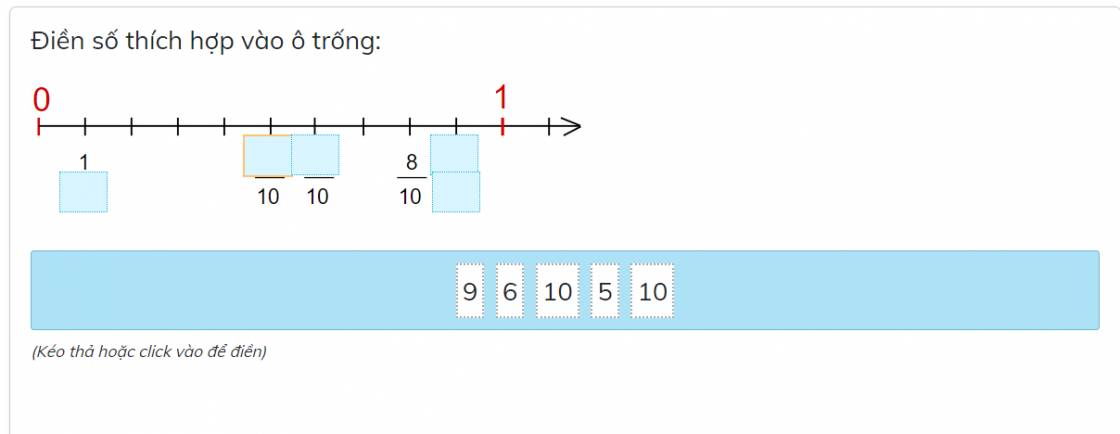
Từ 0 đến 1 được chia thành 10 phần bằng nhau.
Giá trị của mỗi phần là: \(\dfrac{1}{10}\)
Từ lập luận trên ta có:
Số thích hợp để điền vào các ô trống lần lượt là:
10; 5; 6; 9; 10
0 ; 1/10 ; 2/10 ; 3/10 ; 4/10 ; 5/10 ; 6/10 ; 7/10 ; 8/10 ; 9/10 ; 1
Chúc bạn học tốt!




\(\dfrac{14}{25}-\dfrac{3}{5}=\dfrac{14-15}{25}=\dfrac{-1}{25}\)








a: Ta có: ΔOBC cân tại O
mà OH là đường cao
nên OH là phân giác của \(\widehat{BOC}\)
=>OA là phân giác của góc BOC
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}=90^0\)
=>AC là tiếp tuyến của (O)
b: Xét (O) có
ΔCED nội tiếp
CD là đường kính
Do đó: ΔCED vuông tại E
=>CE\(\perp\)ED tại E
=>CE\(\perp\)AD tại E
Xét ΔDCA vuông tại C có CE là đường cao
nên \(AE\cdot AD=AC^2\)
mà AC=AB
nên \(AE\cdot AD=AB^2\)
c: Gọi giao điểm của ON với DE là K
Theo đề, ta có: ON\(\perp\)DE tại K
Ta có: ΔODE cân tại O
mà OK là đường cao
nên K là trung điểm của DE
Xét ΔOKA vuông tại K và ΔOHN vuông tại H có
\(\widehat{KOA}\) chung
Do đó: ΔOKA đồng dạng với ΔOHN
=>\(\dfrac{OK}{OH}=\dfrac{OA}{ON}\)
=>\(OK\cdot ON=OH\cdot OA\)(1)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=OD^2\left(2\right)\)
Từ (1) và (2) suy ra \(OD^2=OK\cdot ON\)
=>\(\dfrac{OD}{OK}=\dfrac{ON}{OD}\)
Xét ΔODN và ΔOKD có
\(\dfrac{OD}{OK}=\dfrac{ON}{OD}\)
\(\widehat{DON}\) chung
DO đó: ΔODN đồng dạng với ΔOKD
=>\(\widehat{ODN}=\widehat{OKD}=90^0\)
=>DN là tiếp tuyến của (O)