K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 12 2023
a: Ta có: ΔOBC cân tại O
mà OH là đường cao
nên OH là phân giác của \(\widehat{BOC}\)
=>OA là phân giác của góc BOC
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}=90^0\)
=>AC là tiếp tuyến của (O)
b: Xét (O) có
ΔCED nội tiếp
CD là đường kính
Do đó: ΔCED vuông tại E
=>CE\(\perp\)ED tại E
=>CE\(\perp\)AD tại E
Xét ΔDCA vuông tại C có CE là đường cao
nên \(AE\cdot AD=AC^2\)
mà AC=AB
nên \(AE\cdot AD=AB^2\)
c: Gọi giao điểm của ON với DE là K
Theo đề, ta có: ON\(\perp\)DE tại K
Ta có: ΔODE cân tại O
mà OK là đường cao
nên K là trung điểm của DE
Xét ΔOKA vuông tại K và ΔOHN vuông tại H có
\(\widehat{KOA}\) chung
Do đó: ΔOKA đồng dạng với ΔOHN
=>\(\dfrac{OK}{OH}=\dfrac{OA}{ON}\)
=>\(OK\cdot ON=OH\cdot OA\)(1)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=OD^2\left(2\right)\)
Từ (1) và (2) suy ra \(OD^2=OK\cdot ON\)
=>\(\dfrac{OD}{OK}=\dfrac{ON}{OD}\)
Xét ΔODN và ΔOKD có
\(\dfrac{OD}{OK}=\dfrac{ON}{OD}\)
\(\widehat{DON}\) chung
DO đó: ΔODN đồng dạng với ΔOKD
=>\(\widehat{ODN}=\widehat{OKD}=90^0\)
=>DN là tiếp tuyến của (O)
10 tháng 10 2021
f: Ta có: \(\sqrt{2-x}=\sqrt{x^2-2x+4}\)
\(\Leftrightarrow x^2-2x+4=2-x\)
\(\Leftrightarrow x^2-x+2=0\)
\(\Leftrightarrow x\in\varnothing\)
TM
1
15 tháng 10 2021
\(1,\\ a,=\dfrac{12\left(3+\sqrt{3}\right)}{6}=2\left(3+\sqrt{3}\right)\\ b,=\dfrac{8\left(\sqrt{5}-2\right)}{1}=8\left(\sqrt{5}-2\right)\\ c,=\dfrac{14\left(\sqrt{10}-\sqrt{3}\right)}{7}=2\left(\sqrt{10}-\sqrt{3}\right)\)
7 tháng 10 2021
4: Ta có: \(\sqrt{3+2\sqrt{2}}+\sqrt{6-4\sqrt{2}}\)
\(=\sqrt{2}+1+2-\sqrt{2}\)
=3
7 tháng 10 2021
5: Ta có: \(2+\sqrt{17-4\sqrt{9}+4\sqrt{5}}\)
\(=2+\sqrt{5+4\sqrt{5}}\)
6: Ta có: \(2\sqrt{3}+\sqrt{2}+\sqrt{18-8\sqrt{2}}\)
\(=2\sqrt{3}+\sqrt{2}+4-\sqrt{2}\)
\(=4+2\sqrt{3}\)
AT
5 tháng 7 2021
a) (d) cắt trục hoành tại điểm có hoành độ bằng 2
\(\Rightarrow\) tọa độ điểm đó là \(\left(2;0\right)\)
\(\Rightarrow0=2a-3\Rightarrow a=\dfrac{3}{2}\Rightarrow\left(d\right):y=\dfrac{3}{2}x-3\)
b) Vì (d) song song với đồ thị của hàm \(y=2x+1\)
\(\Rightarrow\left\{{}\begin{matrix}a=2\\-3\ne1\end{matrix}\right.\Rightarrow a=2\Rightarrow\left(d\right):y=2x-3\)
c) Gọi A là giao điểm của (d) và (d')
\(\Rightarrow x_A=1\Rightarrow y_A=2+3=5\Rightarrow A\left(1;5\right)\)
\(\Rightarrow5=a-3\Rightarrow a=8\Rightarrow\left(d\right):y=8x-3\)
7 tháng 7 2021
a) Thay a=3 vào (d), ta được:
y=3x+b
Vì (d): y=3x+b cắt trục hoành tại điểm có hoành độ bằng 2 nên
Thay x=2 và y=0 vào (d), ta được:
\(3\cdot2+b=0\)
\(\Leftrightarrow b=-6\)
Vậy: (d): y=3x-6
b) Thay a=2 vào (d), ta được:
y=2x+b
Thay x=1 và y=6 vào (d), ta được:
\(b+2\cdot1=6\)
hay b=4
Vậy: (d): y=2x+4
23 tháng 7 2021
a) Ta có: \(\sqrt{12+2\sqrt{35}}-\sqrt{12-2\sqrt{35}}\)
\(=\sqrt{7}+\sqrt{5}-\sqrt{7}+\sqrt{5}\)
\(=2\sqrt{5}\)
b) Ta có: \(\left(\dfrac{5+\sqrt{5}}{\sqrt{5}+1}+2\right)\left(\dfrac{5-\sqrt{5}}{\sqrt{5}-1}-2\right)\)
\(=\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)\)
=1
c) Ta có: \(\dfrac{7\sqrt{2}+2\sqrt{7}}{\sqrt{14}}-\dfrac{5}{\sqrt{7}+\sqrt{2}}\)
\(=\sqrt{7}+\sqrt{2}-\sqrt{7}+\sqrt{2}\)
\(=2\sqrt{2}\)
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
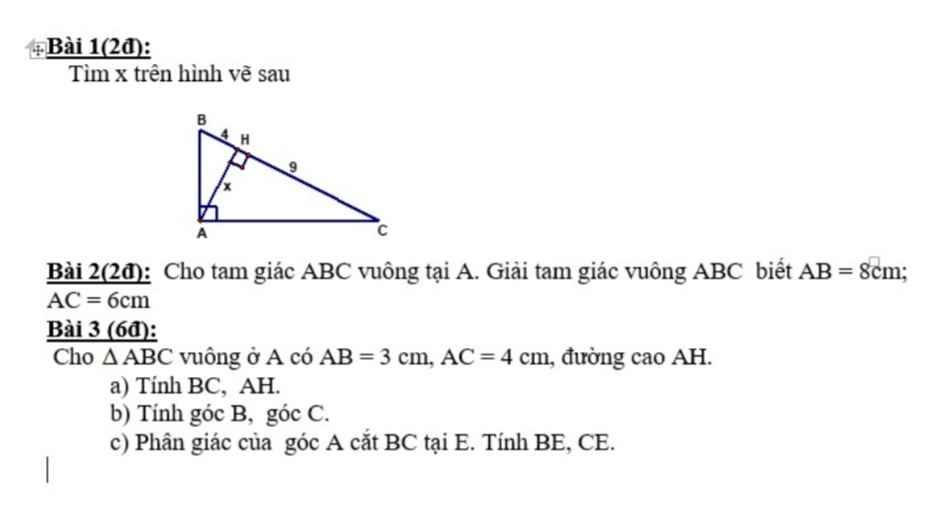
Bài 1:
Áp dụng HTL trong tam giác vuông:
$AH^2=BH.CH$
$\Leftrightarrow x^2=4.9=36$
$\Rightarrow x=6$ (do $x>0$)
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
Bài 2:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
$\sin B=\frac{AC}{BC}=\frac{6}{10}=\frac{3}{5}$
$\Rightarrow \widehat{B}=36,87^0$
$\widehat{C}=90^0-\widehat{B}=90^0-36,87^0=53,13^0$