
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=9+144=153\)
=>\(BC=3\sqrt{17}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}=4\)
=>\(\widehat{B}\simeq75^057'\)
c: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN\(\sim\)ΔACB

\(72.\)
Xét tam giác AHC vuông tại H ta có:
\(\sin C=\dfrac{AH}{AC}\) (Tỉ số lượng giác).
\(\Rightarrow\sin30^o=\dfrac{AH}{40}.\Rightarrow AH=20.\)
Xét tam giác AHB vuông tại H:
\(AB^2=AH^2+BH^2\left(Pytago\right).\)
\(\Rightarrow29^2=20^2+BH^2.\\ \Leftrightarrow BH^2=29^2-20^2.\\ \Rightarrow BH=21.\)

Câu 2 :
a. \(n_C=\dfrac{3.6}{12}=0,3\left(mol\right)\)
\(n_{O_2}=\dfrac{4.48}{22,4}=0,2\left(mol\right)\)
Ta thấy : 0,3 > 0,2 => C dư , O2 đủ
PTHH : C + O2 -> CO2
0,2 0,2 0,2
b. \(m_{CO_2}=0,2.44=8,8\left(g\right)\)
c.\(m_{O_2\left(dư\right)}\left(0,3-0,2\right).32=3,2\left(g\right)\)

Y x 9,25 + 75% x Y = 55,35
Y x 9,25 + 0,75 x Y = 55,35
Y x ( 9,25 + 0,75 ) = 55,35
Y x 10 = 55,35
Y = 55,35 : 10
Y = 5,535

????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
Chỗ này là để hỏi bài hay hoặc khó chứ ko phải là chỗ để tìm người nếu muốn thì cứ lên đồn công an mà hỏi nhé bạn

14: \(=\dfrac{4x+7+1}{\left(x+2\right)\left(4x+7\right)}=\dfrac{4}{4x+7}\)



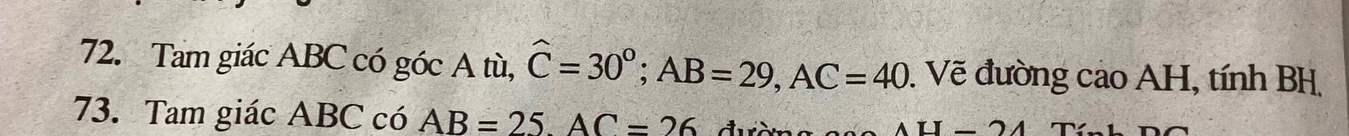 bài 72 giúp em 🥲🥲
bài 72 giúp em 🥲🥲




a, Xét tứ giác ABCD có : BM = MC; DM = MA
⇒ Tứ giác ABCD là hình bình hành vì tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
Vì ABCD là hình bình hành có một góc vuông nên ABCD là HCN (đpcm)
⇒ AB // CD; AB = CD
b, Xét tứ giác BEDC có:
BE // CD
BE = AB = CD
⇒ BEDC là hình bình hành (vì một tứ giác có một cặp cạnh đối diện song song và bằng nhau thì tứ giác đó là hình bình hành)
c, Xét tam giác ADE có:
AM = MD;
AB = BE;
⇒ BM là đường trung bình của tam giác ADE
⇒ BM = \(\dfrac{1}{2}\) DE
⇒ \(\dfrac{BM}{DE}\) = \(\dfrac{1}{2}\) (1)
BM // DE
Theo hệ quả của talet ta có:
\(\dfrac{MK}{KE}\) = \(\dfrac{BM}{DE}\) (2)
Kết hợp (1) và (2) ta có:
\(\dfrac{MK}{KE}\) = \(\dfrac{1}{2}\)
KE = 2.MK (đpcm)