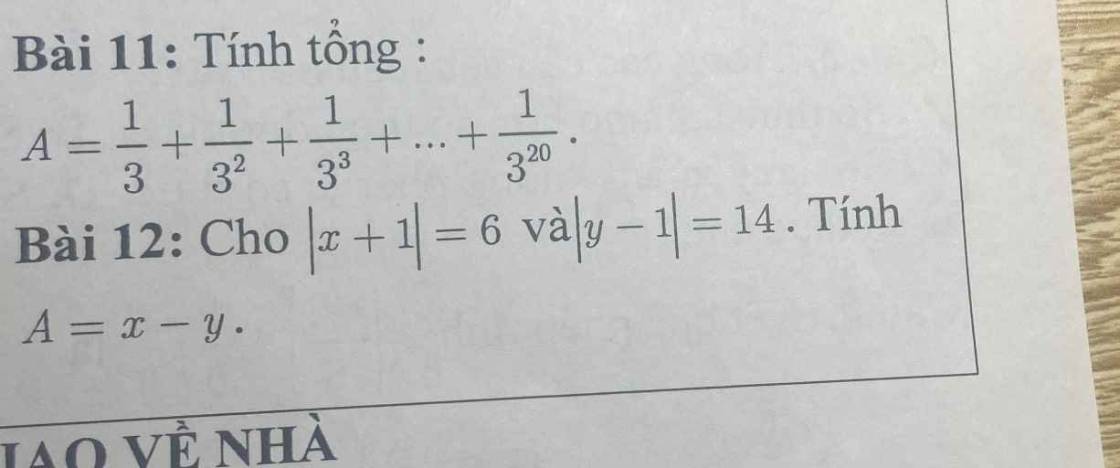
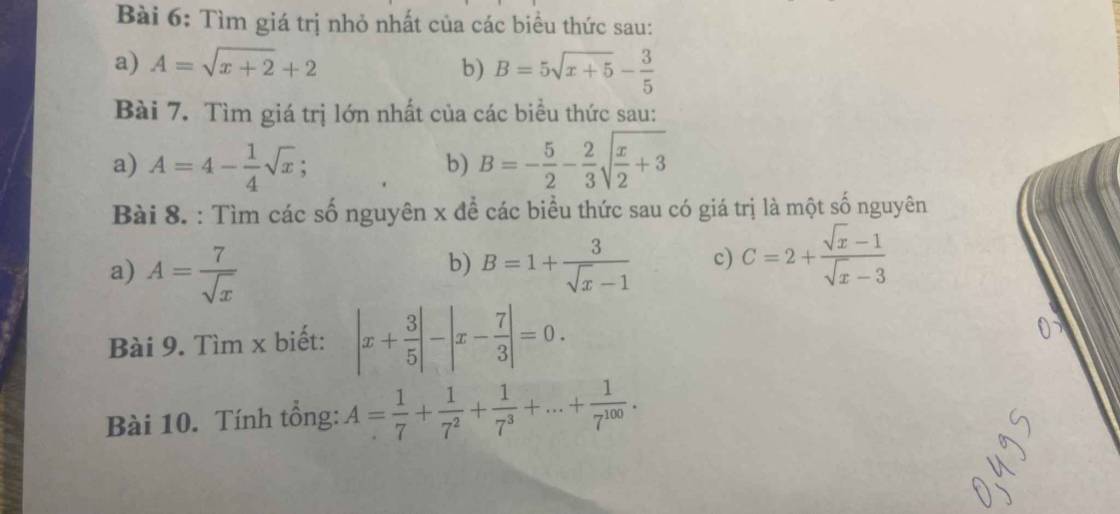
Lm giúp mk mấy bài trên đi, mk đang cần gấp.Xin cảm...
Đọc tiếp
Lm giúp mk mấy bài trên đi, mk đang cần gấp.Xin cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 11 2023
5B:
a: Xét ΔABC và ΔEBF có
BA=BE
\(\widehat{ABC}=\widehat{EBF}\)
BC=BF
Do đó: ΔABC=ΔEBF
b: ΔABC=ΔEBF
=>\(\widehat{BAC}=\widehat{BEF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//EF
Xét tứ giác ACEF có
B là trung điểm chung của AE và CF
Do đó: ACEF là hình bình hành
=>AF//CE
c: Xét tứ giác AMEN có
AM//EN
AM=EN
Do đó: AMEN là hình bình hành
=>AE cắt MN tại trung điểm của mỗi đường
mà B là trung điểm của AE
nên B là trung điểm của MN
=>M,B,N thẳng hàng
5 tháng 11 2023
Bài 3:
a: Đặt \(\widehat{B}=b;\widehat{C}=c\)
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(b+c+80^0=180^0\)
=>\(b+c=100^0\)
mà b-c=20
nên \(\left\{{}\begin{matrix}b=\dfrac{100+20}{2}=60\\c=60-20=40\end{matrix}\right.\)
Vậy: \(\widehat{B}=60^0;\widehat{C}=40^0\)
b: AD là phân giác của \(\widehat{BAC}\)
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{1}{2}\cdot\widehat{BAC}=\dfrac{1}{2}\cdot80^0=40^0\)
Xét ΔADC có \(\widehat{ADB}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADB}=\widehat{DAC}+\widehat{C}\)
=>\(\widehat{ADB}=40^0+40^0=80^0\)
4:
a: Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{BAC}+20^0+40^0=180^0\)
=>\(\widehat{BAC}=120^0\)
=>ΔABC là tam giác tù
b: AD nằm giữa AB và AC
=>\(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}=120^0\)
mà \(\widehat{CAD}=2\cdot\widehat{BAD}\)
nên \(\widehat{CAD}=\dfrac{2}{3}\cdot120^0=80^0\)
=>\(\widehat{BAD}=\dfrac{1}{2}\cdot80^0=40^0\)
Xét ΔABD có \(\widehat{ADC}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADC}=\widehat{BAD}+\widehat{B}=40^0+20^0=60^0\)
7 tháng 7 2023
2:
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>DE=AH=12cm
b: ΔAHB vuông tại H có HD vuông góc AB
nên AD*AB=AH^2
ΔAHC vuông tại H có HE vuông góc AC
nên AE*AC=AH^2
=>AD*AB=AE*AC
c: góc IAC+góc AED
=góc ICA+góc AHD
=góc ACB+góc ABC=90 độ
=>AI vuông góc ED
4:
a: góc BDH=góc BEH=góc DBE=90 độ
=>BDHE là hình chữ nhật
b: BDHE là hình chữ nhật
=>góc BED=góc BHD=góc A
Xét ΔBED và ΔBAC có
góc BED=góc A
góc EBD chung
=>ΔBED đồng dạng với ΔBAC
=>BE/BA=BD/BC
=>BE*BC=BA*BD
c: góc MBC+góc BED
=góc C+góc BHD
=góc C+góc A=90 độ
=>BM vuông góc ED
QM
2
QM
1
QM
1
QM
1
1 tháng 7 2023
a: (x-4)(x+5)>0
=>x-4>0 hoặc x+5<0
=>x>4 hoặc x<-5
b: (2x+1)(x-3)<0
=>2x+1>0 và x-3<0
=>-1/2<x<3
c: (x-7)(3-x)<0
=>(x-7)(x-3)>0
=>x>7 hoặc x<3
d: x^2+6x-16<0
=>(x+8)(x-2)<0
=>-8<x<2
e: 3x^2+7x+4<0
=>3x^2+3x+4x+4<0
=>(x+1)(3x+4)<0
=>3x+4>0 và x+1<0
=>-4/3<x<-1
f: 5x^2-9x+4>0
=>(x-1)(5x-4)>0
=>x>1 hoặc x<4/5
g: x^2+6x-16<0
=>(x+8)(x-2)<0
=>-8<x<2
h: x^2+4x-21>0
=>(x+7)(x-3)>0
=>x>3 hoặc x<-7
i: x^2-9x-22<0
=>(x-11)(x+2)<0
=>-2<x<11
l: 16x^2+40x+25<0
=>(2x+5)^2<0(loại)
m: 3x^2-4x-4>=0
=>3x^2-6x+2x-4>=0
=>(x-2)(3x+2)>=0
=>x>=2 hoặc x<=-2/3
NH
3
Bài 11:
\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{20}}\)
=>\(3\cdot A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{19}}\)
=>\(3\cdot A-A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{19}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^{19}}-\dfrac{1}{3^{20}}\)
=>\(2A=1-\dfrac{1}{3^{20}}=\dfrac{3^{20}-1}{3^{20}}\)
=>\(A=\dfrac{3^{20}-1}{2\cdot3^{20}}\)
Bài 6:
a: ĐKXĐ: x>=-2
\(\sqrt{x+2}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(\sqrt{x+2}+2>=2\forall x\) thỏa mãn ĐKXĐ
=>\(A>=2\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x+2=0
=>x=-2
Vậy: \(A_{min}=2\) khi x=-2
b: ĐKXĐ: x>=-5
\(\sqrt{x+5}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(5\sqrt{x+5}>=0\forall x\)thỏa mãn ĐKXĐ
=>\(5\sqrt{x+5}-\dfrac{3}{5}>=-\dfrac{3}{5}\forall x\) thỏa mãn ĐKXĐ
=>\(B>=-\dfrac{3}{5}\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x+5=0
=>x=-5
vậy: \(B_{min}=-\dfrac{3}{5}\) khi x=-5