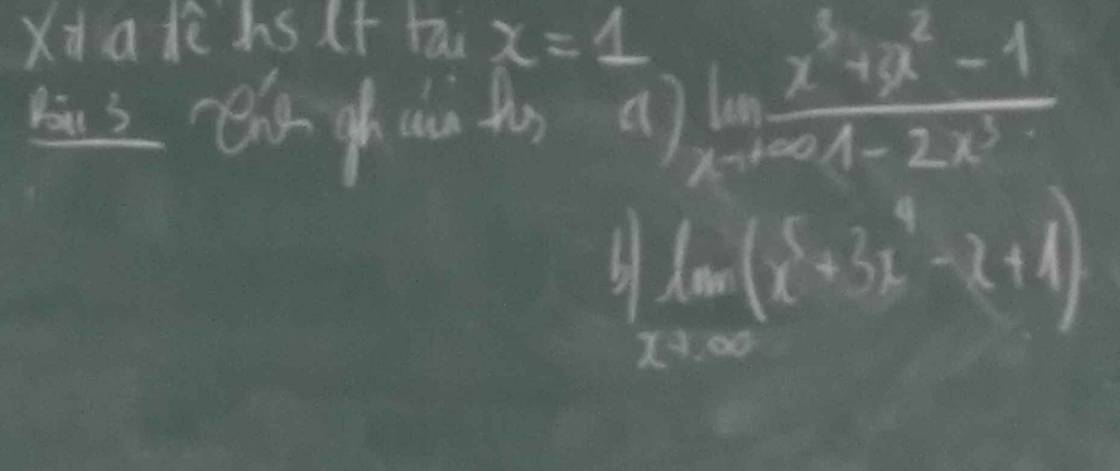Giúp mình giải bài tập này với các bạn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 5 2023
4:
\(n\left(\Omega\right)=C^3_{35}\)
\(n\left(A\right)=C^3_{15}\)
=>\(P\left(A\right)=\dfrac{13}{187}\)
14 tháng 4 2023
a: \(\Leftrightarrow\left\{{}\begin{matrix}2x+2y-2z=2\\2x-y+2z=2\\2x-6y+2z=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+y=4\\4x-4y=2\\x-3y+z=0\end{matrix}\right.\)
=>x=9/10 và y=2/5 và z=3/10
b: \(\Leftrightarrow\left\{{}\begin{matrix}2x-2y=2\\2x+z=2\\y+3z=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2y-z=0\\y+3z=3\\x-y=1\end{matrix}\right.\)
=>y=-3/5 và z=6/5 và x=1+(-3/5)=2/5
c: \(\Leftrightarrow\left\{{}\begin{matrix}4x-4y-4z=2\\12x+4y-4z=0\\4x+3y-4z=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-8x-8y=2\\x-7y=-1\\3x+y-z=0\end{matrix}\right.\)
=>x=-11/32; y=3/32; z=-15/16
11 tháng 5 2023
1: 
2: =>x>=0 và 4x^2=x-1
=>4x^2-x+1=0 và x>=0
=>\(x\in\varnothing\)
17 tháng 4 2023
2:=n^3-n+12n
=n(n-1)(n+1)+12n
Vì n;n-1;n+1 là 3 số nguyên
nên n(n-1)(n+1) chia hết cho 3!=6
=>A chia hết cho 6
KV
17 tháng 4 2023
Câu a xem lại đề em nhé
b) Ta có:
\(n^3+11n=n^3+n-12n\)
\(=n\left(n^2-1\right)+12n\)
\(=n\left(n-1\right)\left(n+1\right)+12n\)
Do \(n\left(n-1\right)\) là tích của hai số nguyên liên tiếp nên chia hết cho 2
Do \(n\left(n-1\right)\left(n+1\right)\) là tích của ba số nguyên liên tiếp nên chia hết cho 3
\(\Rightarrow n\left(n-1\right)\left(n+1\right)⋮6\)
Lại có \(12n⋮6\)
\(\Rightarrow\left[n\left(n-1\right)\left(n+1\right)+12n\right]⋮6\)
Vậy \(\left(n^3-11n\right)⋮6\)
KV
17 tháng 4 2023
Sửa đề câu a
\(\left(4^n+15n-1\right)⋮9\)
Giải
Đặt \(A_n=4^n+15n-1\)
- Với n = 1 \(\Rightarrow A_1=4+15-1=18⋮9\)
- Giả sử đúng với \(n=k\ge1\) nghĩa là:
\(A_k=\left(4^k+15k-1\right)⋮9\) (giả thiết quy nạp)
Ta cần chứng minh: \(A_{k+1}⋮9\)
Thật vậy, ta có:
\(A_{k+1}=4^{k+1}+15\left(k+1\right)-1\)
\(=4.4^k+15k+15-1\)
\(=4\left(4^k+15k-1\right)-45k+4+15-1\)
\(=4\left(4^k+15k-1\right)-45k+18\)
\(=4A_k-45k+18\)
Do \(A_k⋮9\)
\(-45k+18=-9\left(5k-2\right)⋮9\)
\(\Rightarrow A_{k+1}=\left(4A_k-45k+18\right)⋮9\)
Vậy \(\left(4^n+15n-1\right)⋮9\) \(\forall n\in N\)*
H9
HT.Phong (9A5)
CTVHS
17 tháng 4 2023
Bạn tham khảo link này nhé:
https://khoahoc.vietjack.com/question/275699/chung-minh-rang-voi-n-thuoc-n-n-3-11n-chia-het-cho-6
17 tháng 4 2023
n^3+11n=n^3-n+12n
=n(n-1)(n+1)+12n
Vì n;n-1;n+1 là 3 số liên tiếp
nên n(n-1)(n+1) chia hết cho 3!=6
=>A chia hết cho 6
17 tháng 4 2023
A=4^n+15n-1
Khi n=1 thì A=4+15-1=18 chia hết cho 9
Giả sử n=k>1 thì giả sử Ak chia hết cho 9
Ta cần chứng minh Ak+1 chia hêt cho 9
\(A_{k+1}=4^{k+1}+15\left(k+1\right)-1\)
\(=4^k\cdot4+15k+15-1\)
\(=4\cdot A_k+\left(-45k+18\right)⋮9\)
=>A chia hết cho 9
17 tháng 4 2023
5: 3n^2+6=3(n^2+2) chia hết cho 3
4:
4n^2+4n-2=2(2n^2+2n-1) chia hêt cho 2
LH
17 tháng 4 2023
n^3-n+3 chia hết cho 3
n(n^2-1)+3
n(n-1)(n+1) +3
mà n (n-1)(n+1) là tích 3 số liên tiếp luôn chia hết cho 3
=> n^3-n+3 chia hết cho 3
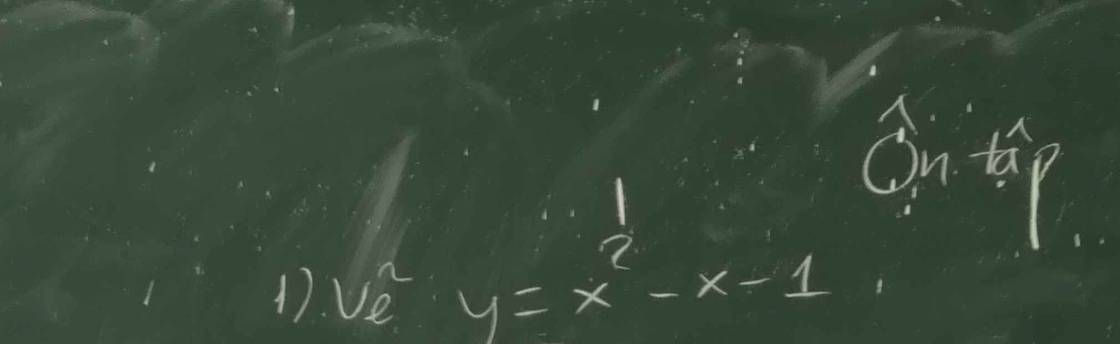
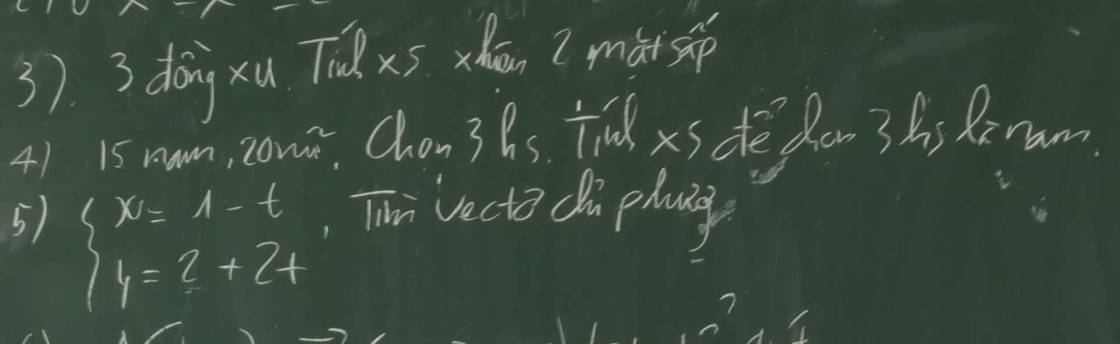
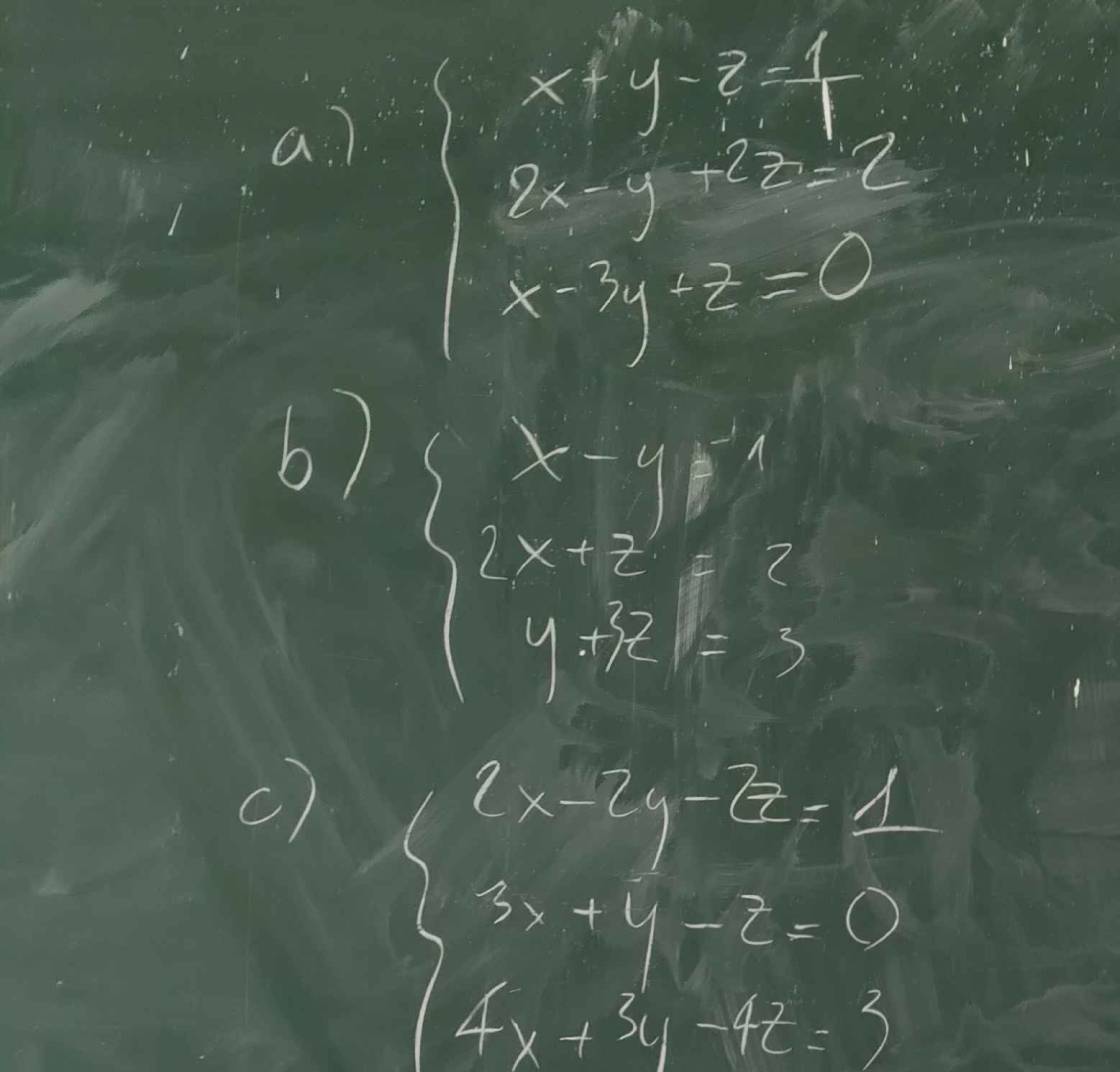
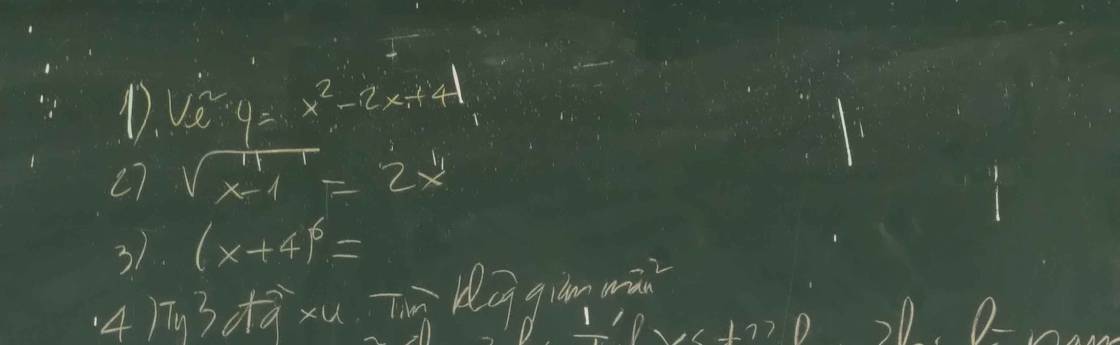
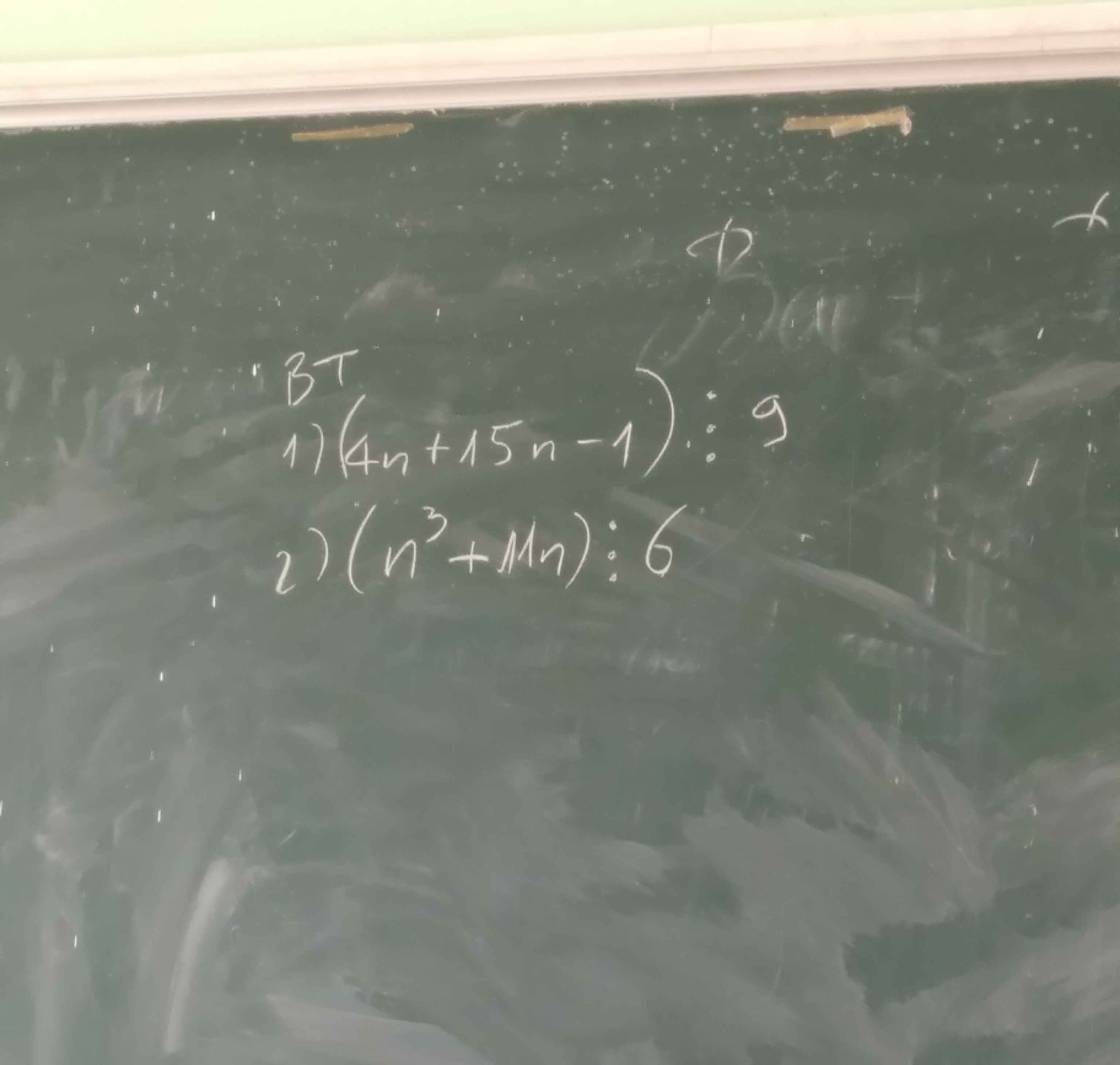
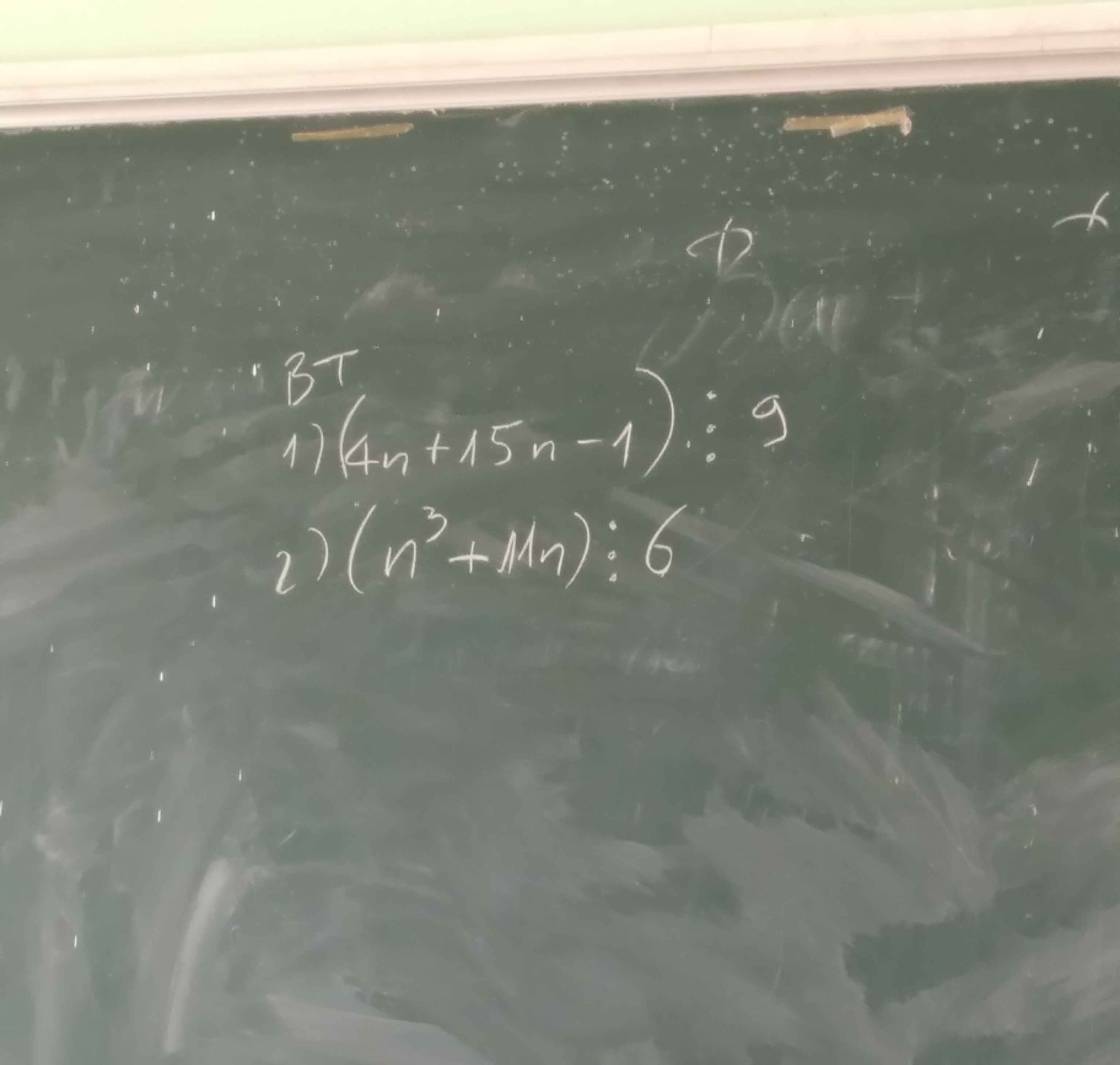
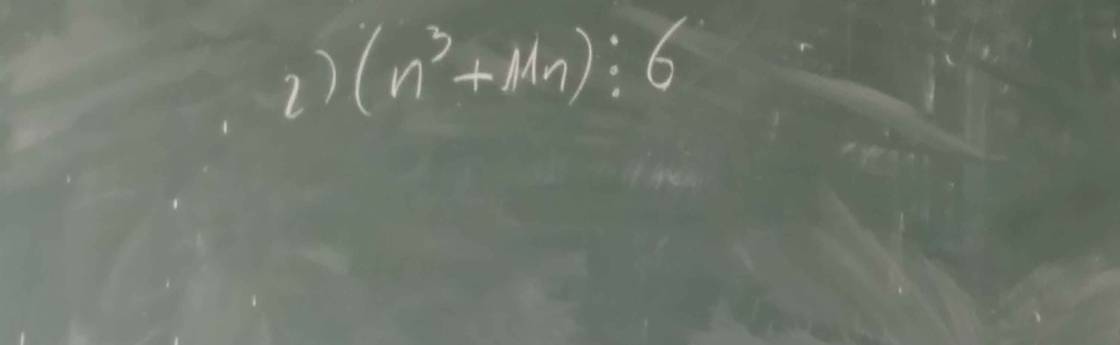
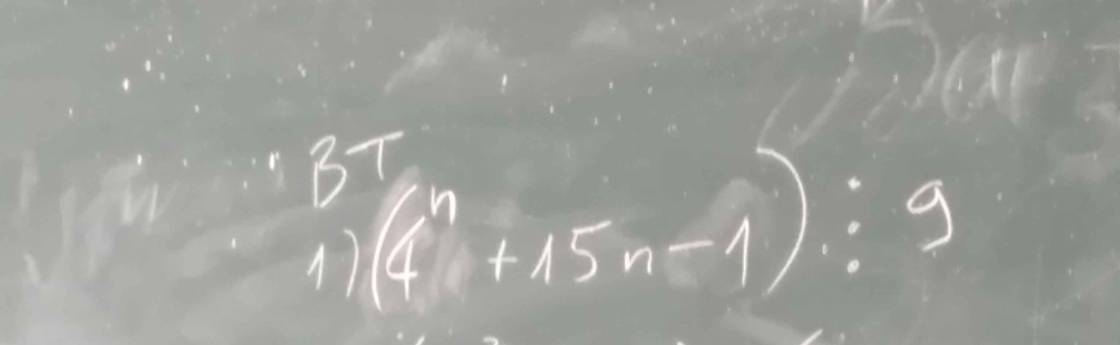
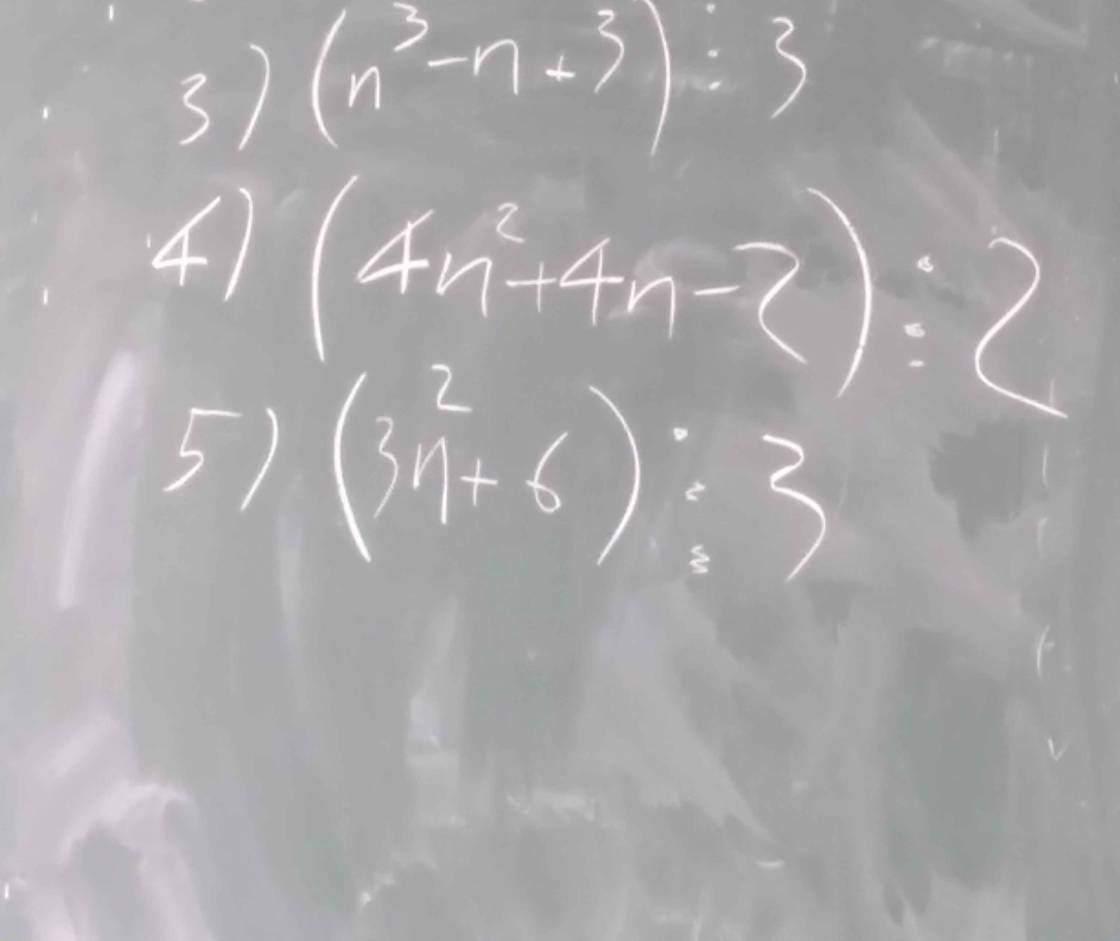
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{x^3+x^2-1}{-2x^3+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{1+\dfrac{1}{x}-\dfrac{1}{x^3}}{-2+\dfrac{1}{x^3}}=\dfrac{1}{-2}=-\dfrac{1}{2}\)
b: \(\lim\limits_{x\rightarrow-\infty}\left(x^5+3x^4-x+1\right)\)
\(=\lim\limits_{x\rightarrow-\infty}\left[x^5\left(1+\dfrac{3}{x}-\dfrac{1}{x^4}+\dfrac{1}{x^5}\right)\right]\)
\(=-\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\infty}x^5=-\infty\\\lim\limits_{x\rightarrow-\infty}1+\dfrac{3}{x}-\dfrac{1}{x^4}+\dfrac{1}{x^5}=1>0\end{matrix}\right.\)