giúp tôi với mn ơi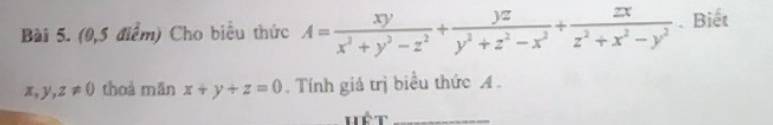
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
29 tháng 9 2023
Bài 1
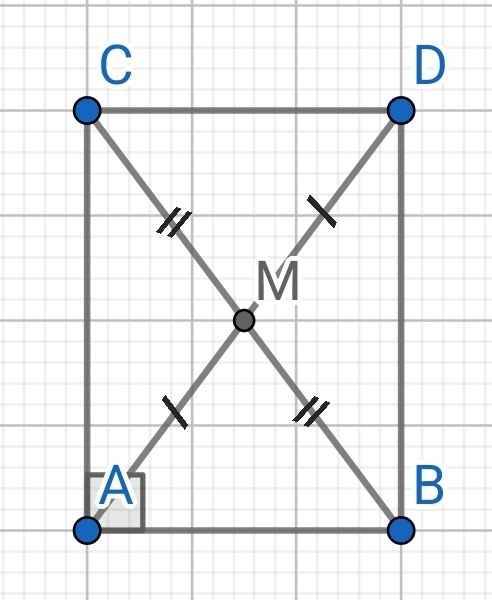a) Do AM là đường trung tuyến của ∆ABC
⇒ M là trung điểm BC
Do MA = MD (gt)
⇒ M là trung điểm AD
Tứ giác ABDC có:
M là trung điểm BC (cmt)
M là trung điểm AD (cmt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (gt)
⇒ ABDC là hình chữ nhật
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC của ∆ABC
⇒ AM = BC : 2
= 10 : 2
= 5 (cm)
c) Nếu ∠B = 45⁰
⇒ C = 90⁰ - ∠B
= 90⁰ - 45⁰
= 45⁰
⇒ ∆ABC vuông cân tại A
⇒ AB = AC
Lại có ABDC là hình chữ nhật
⇒ ABDC là hình vuông
KV
29 tháng 9 2023
Bài 2
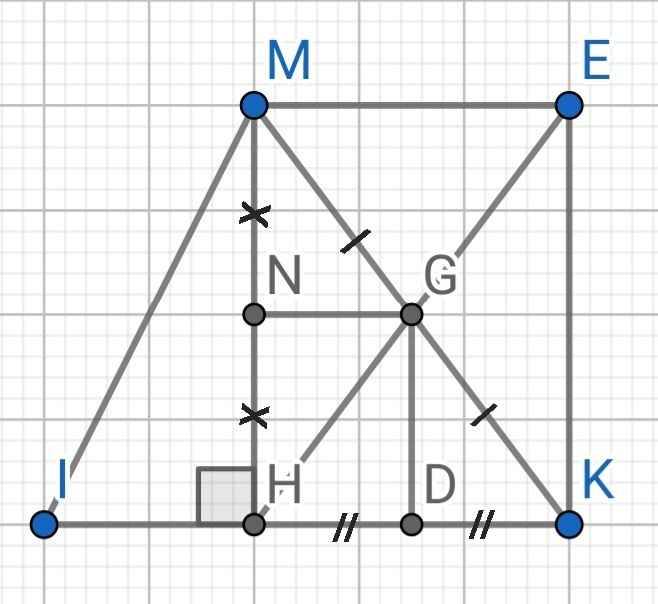a) Do H và E đối xứng với nhau qua G (gt)
⇒ G là trung điểm của HE
Tứ giác MEKH có:
G là trung điểm HE (cmt)
G là trung điểm MK (gt)
⇒ MEKH là hình bình hành
Mà ∠MHK = 90⁰ (MH ⊥ IK)
⇒ MEKH là hình chữ nhật
b) ∆MHK có:
N là trung điểm MH (gt)
G là trung điểm MK (gt)
⇒ NG là đường trung bình của ∆MHK
⇒ NG // HK và NG = HK : 2
Do D là trung điểm HK
⇒ HD = HK : 2
⇒ HD = NG = HK : 2
Do NG // HK
⇒ NG // HD
Do ∠MHK = 90⁰
⇒ ∠NHD = 90⁰
Tứ giác NGDH có:
NG // HD (cmt)
NG = HD (cmt)
⇒ NGDH là hình bình hành
Mà ∠NHD = 90⁰ (cmt)
⇒ NGDH là hình chữ nhật
M
2
AH
Akai Haruma
Giáo viên
31 tháng 7 2023
Lời giải:
$A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{19.20}$
$=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+...+\frac{20-19}{19.20}$
$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{19}-\frac{1}{20}$
$=1-\frac{1}{20}=\frac{19}{20}$
NT
3
LH
0
ND
1
24 tháng 9 2021
a: \(-\dfrac{1}{21}-\dfrac{1}{14}=\dfrac{-14-21}{294}=\dfrac{-35}{294}=-\dfrac{5}{42}\)
b: \(\dfrac{-1}{9}-\dfrac{5}{12}=\dfrac{-12-45}{108}=\dfrac{-57}{108}=\dfrac{-19}{36}\)
c: \(\dfrac{-14}{20}+\dfrac{3}{5}=\dfrac{-7}{10}+\dfrac{6}{10}=\dfrac{-1}{10}\)
A
10
KV
28 tháng 9 2023
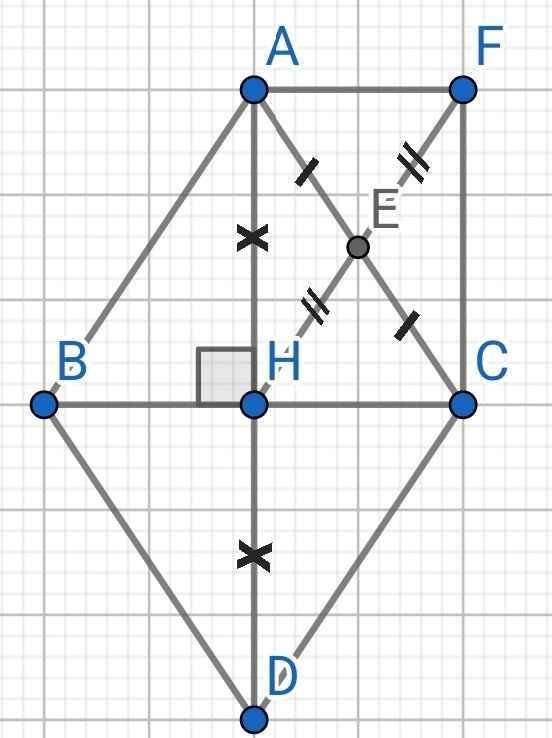a) Do ∆ABC cân tại A có AH là đường cao
⇒ AH cũng là đường trung tuyến của ∆ABC
⇒ H là trung điểm của BC
Lại có HD = HA (gt)
⇒ H là trung điểm của AD
Ta có:
AH ⊥ BC
⇒ AD ⊥ BC
Xét tứ giác ABDC có:
H là trung điểm của BC (cmt)
H là trung điểm của AD (cmt)
⇒ ABDC là hình bình hành
Mà AD ⊥ BC (cmt)
⇒ ABDC là hình thoi
b) Do H là trung điểm của BC (cmt)
⇒ BH = BC : 2 = 6 : 2 = 3 (cm)
∆ABH vuông tại H (do AH ⊥ BC)
⇒ AB² = AH² + BH² (Pytago)
⇒ AH² = AB² - BH²
= 5² - 3²
= 16
⇒ AH = 4 (cm)
⇒ AD = AH = 4 (cm)
c) Tứ giác AHCF có:
E là trung điểm AC (gt)
E là trung điểm FH (gt)
⇒ AHCF là hình bình hành
Mà ∠AHC = 90⁰ (AH ⊥ BC)
⇒ AHCF là hình chữ nhật
⇒ AF ⊥ AH và FC ⊥ CH
d) Do ABDC là hình thoi (cmt)
⇒ ∠BAC = ∠BDC = 60⁰
Ta có:
∠BAC + ∠BDC + ∠ABD + ∠ACD = 360⁰ (tổng các góc của hình thoi ABDC)
⇒ ∠ABD + ∠ACD = 360⁰ - (∠BAC + ∠BDC)
= 360⁰ - (60⁰ + 60⁰)
= 360⁰ - 120⁰
= 240⁰
Mà ∠ABD = ∠ACD (hai góc đối của hình thoi ABDC)
⇒ ∠ABD = ∠ACD = 240⁰ : 2 = 120⁰
Vậy các góc của hình thoi ABDC lần lượt là:
∠BAC = ∠BDC = 60⁰
∠ABD = ∠ACD = 120⁰
Lời giải:
$x+y+z=0\Rightarrow x+y=-z$. Khi đó:
$x^2+y^2-z^2=(x+y)^2-2xy-z^2=(-z)^2-2xy-z^2=-2xy$
Tương tự: $y^2+z^2-x^2=-2yz, z^2+x^2-y^2=-2xz$
Khi đó:
$A=\frac{xy}{-2xy}+\frac{yz}{-2yz}+\frac{zx}{-2zx}=\frac{1}{-2}+\frac{1}{-2}+\frac{1}{-2}=\frac{-3}{2}$