cứu tuiiiiiii,tui tick cho
K
Khách
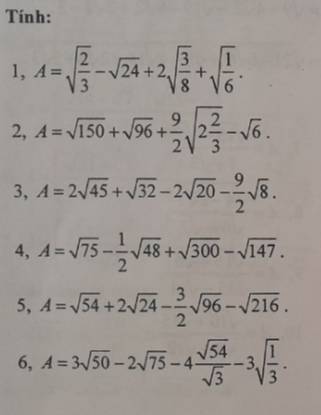
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 11 2023
10: \(\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=\left(\sqrt{3-\sqrt{5}}\right)^2+\left(\sqrt{3+\sqrt{5}}\right)^2+2\cdot\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\cdot\sqrt{9-5}\)
\(=6+2\cdot2=10\)
11: \(\left(\sqrt{\sqrt{7}+\sqrt{3}}+\sqrt{\sqrt{7}-\sqrt{3}}\right)^2\)
\(=\left(\sqrt{\sqrt{7}+\sqrt{3}}\right)^2+\left(\sqrt{\sqrt{7}-\sqrt{3}}\right)^2+2\cdot\sqrt{\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)}\)
\(=\sqrt{7}+\sqrt{3}+\sqrt{7}-\sqrt{3}+2\cdot\sqrt{7-3}\)
\(=2\sqrt{7}+2\cdot2=2\sqrt{7}+4\)
12: \(\left(\sqrt{\sqrt{11}+\sqrt{7}}-\sqrt{\sqrt{11}-\sqrt{7}}\right)^2\)
\(=\left(\sqrt{\sqrt{11}+\sqrt{7}}\right)^2+\left(\sqrt{\sqrt{11}-\sqrt{7}}\right)^2-2\cdot\sqrt{\left(\sqrt{11}-\sqrt{7}\right)\left(\sqrt{11}+\sqrt{7}\right)}\)
\(=\sqrt{11}+\sqrt{7}+\sqrt{11}-\sqrt{7}-2\cdot\sqrt{11-7}\)
\(=2\sqrt{11}-4\)
13:
\(\sqrt{\sqrt{2}-1}\cdot\sqrt{2-\sqrt{3-\sqrt{2}}}\cdot\sqrt{2+\sqrt{3-\sqrt{2}}}\)
\(=\sqrt{\sqrt{2}-1}\cdot\sqrt{4-\left(3-\sqrt{2}\right)}\)
\(=\sqrt{\sqrt{2}-1}\cdot\sqrt{\sqrt{2}+1}\)
\(=\sqrt{2-1}=1\)
14:
\(\sqrt{4+\sqrt{8}}\cdot\sqrt{2+\sqrt{2+\sqrt{2}}}\cdot\sqrt{2-\sqrt{2+\sqrt{2}}}\)
\(=\sqrt{4+2\sqrt{2}}\cdot\sqrt{\left(2+\sqrt{2+\sqrt{2}}\right)\left(2-\sqrt{2+\sqrt{2}}\right)}\)
\(=\sqrt{4+2\sqrt{2}}\cdot\sqrt{4-2-\sqrt{2}}\)
\(=\sqrt{\left(4+2\sqrt{2}\right)\left(2-\sqrt{2}\right)}\)
\(=\sqrt{8-4\sqrt{2}+4\sqrt{2}-4}=\sqrt{4}=2\)
G
18
N
5
BD
29 tháng 3 2023
12 phút 48 giây = 768
3,4 giờ = 3 giờ 24 phút
5,7 giờ = 5 giờ 42 phút
\(\dfrac{5}{6}\)phút = 50 giây
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
29 tháng 3 2023
12 phút 48 giây = 12 phút + \(\dfrac{48}{60}\) phút = 12,8 phút
3,4 giờ = 3 giờ + 60 phút \(\times\) 0,4 = 3 giờ 24 phút
5,7 giờ = 5 giờ + 60 phút \(\times\) 0,7 = 5 giờ 42 phút
\(\dfrac{5}{6}\) phút = \(60\) giây \(\times\) \(\dfrac{5}{6}\) = 50 giây
CH
23 tháng 11 2023
\(\text{Giải:}\)
\(\text{Gọi x là số sách cần tìm}\left(x\inℕ^∗;100\le x\le200\right)\)
\(\text{Ta có}:x:3\text{dư}1\Rightarrow x+1⋮3\)
\(\text{x:5 dư 1 => x+1 5}\text{x:5 dư 1 => x+1 5}\text{dư}1\Rightarrow x+1⋮5\)
\(x:7\text{dư}1\Rightarrow x+1⋮7\)
\(\text{=> x+1 BC(3,5,7)}\)
\(\text{Ta lại có 3,5,7 nguyên tố cùng nhau từng đôi một}\)
\(\text{=> BCNN(3,5,7) = 3.5.7 = 105}\)
\(\)\(\)\(\)\(\Rightarrow BC\left(3,5,7\right)=B\left(105\right)=\left\{0;105;210;...\right\}\)
\(\Rightarrow x\in\left\{0;105;210;...\right\}\)
\(\text{Mà}100\le x\le200\Rightarrow x=105\)
\(\text{Vậy trường X mua về 105 quyển sách.}\)
cứu cứu xong tui tăng sp cho
1: \(A=\sqrt{\dfrac{2}{3}}-\sqrt{24}+2\cdot\sqrt{\dfrac{3}{8}}+\sqrt{\dfrac{1}{6}}\)
\(=\sqrt{\dfrac{6}{9}}-2\sqrt{6}+2\cdot\sqrt{\dfrac{6}{16}}+\sqrt{\dfrac{6}{36}}\)
\(=\dfrac{1}{3}\sqrt{6}-2\sqrt{6}+\dfrac{1}{2}\sqrt{6}+\dfrac{1}{6}\sqrt{6}\)
\(=-\sqrt{6}\)
2: \(A=\sqrt{150}+\sqrt{96}+\dfrac{9}{2}\cdot\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
\(=5\sqrt{6}+4\sqrt{6}+\dfrac{9}{2}\cdot\sqrt{\dfrac{8}{3}}-\sqrt{6}\)
\(=8\sqrt{6}+\dfrac{9}{2}\cdot\dfrac{2\sqrt{2}}{\sqrt{3}}\)
\(=8\sqrt{6}+3\sqrt{3}\cdot\sqrt{2}=11\sqrt{6}\)
3: \(A=2\sqrt{45}+\sqrt{32}-2\sqrt{20}-\dfrac{9}{2}\cdot\sqrt{8}\)
\(=2\cdot3\sqrt{5}+4\sqrt{2}-2\cdot2\sqrt{5}-\dfrac{9}{2}\cdot2\sqrt{2}\)
\(=6\sqrt{5}-4\sqrt{5}+4\sqrt{2}-9\sqrt{2}\)
\(=2\sqrt{5}-5\sqrt{2}\)
4: \(A=\sqrt{75}-\dfrac{1}{2}\cdot\sqrt{48}+\sqrt{300}-\sqrt{147}\)
\(=5\sqrt{3}-\dfrac{1}{2}\cdot4\sqrt{3}+10\sqrt{3}-7\sqrt{3}\)
\(=8\sqrt{3}-2\sqrt{3}=6\sqrt{3}\)
5: \(A=\sqrt{54}+2\sqrt{24}-\dfrac{3}{2}\cdot\sqrt{96}-\sqrt{216}\)
\(=3\sqrt{6}+2\cdot2\sqrt{6}-6\sqrt{6}-\dfrac{3}{2}\cdot4\sqrt{6}\)
\(=-3\sqrt{6}+4\sqrt{6}-6\sqrt{6}\)
\(=-5\sqrt{6}\)
6: \(A=3\sqrt{50}-2\sqrt{75}-4\cdot\dfrac{\sqrt{54}}{\sqrt{3}}-3\sqrt{\dfrac{1}{3}}\)
\(=3\cdot5\sqrt{2}-2\cdot5\sqrt{3}-4\cdot\sqrt{18}-\sqrt{3}\)
\(=15\sqrt{2}-10\sqrt{3}-12\sqrt{2}-\sqrt{3}\)
\(=3\sqrt{2}-11\sqrt{3}\)