Tính tổng của A = 7 + 71 + 72 + 73 + .... + 7100
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LN
6
TN
Trần Nguyễn Phương Thảo
CTVHS
VIP
21 tháng 6 2023
F = 7 + 72 + 73 + 74 + ..... + 7100
F= 7+(1+7)+73+(1+7)+...+799+(1+7)
F = 7x8+73x8+...+799x8
F= 8x(7+73+...+799)
mà 8 chia hết 8 => 8(7+73+...+799) chia hết 8
Vậy F chia hết cho 8
CT
1
12 tháng 11 2021
M = 7 + 72 + 73 + 74 + ..... + 7100
M = 7+(1+7)+73+(1+7)+...+799+(1+7)
M = 7x8+73x8+...+799x8
M = 8x(7+73+...+799)
mà 8 chia hết 8 => 8(7+73+...+799) chia hết 8
Vậy M chia hết cho 8
ND
2
1 tháng 5 2022
umm, bn nhân A với 1/7 và nhân B với 1/9, sau đó tính ra và so sánh thôi
M
7 tháng 9 2023
Để chứng minh S chia hết cho 2 và S chia hết cho 57, ta sẽ xem xét từng thành phần trong công thức của S.
Đầu tiên, ta xét dãy từ 71 đến 72025. Trong dãy này, có 72025 - 71 + 1 = 71955 số.
Ta biết rằng nếu một số chia hết cho 2, thì số đó là số chẵn. Trong dãy từ 71 đến 72025, ta có 2 số lẻ liên tiếp (71 và 72), sau đó là 2 số chẵn liên tiếp (73 và 74), và tiếp tục lặp lại quy luật này. Vì vậy, trong 71955 số này, ta có 71955/2 = 35977.5 cặp số chẵn và lẻ.
Do đó, tổng của các số chẵn trong dãy này là 35977.5 * 2 = 71955.
Tiếp theo, ta xét số 72024. Ta biết rằng 72024 chia hết cho 2.
Cuối cùng, ta xét số 72025. Ta biết rằng 72025 chia hết cho 57, vì 72025 = 57 * 1265.
Vậy tổng S chia hết cho 2 và chia hết cho 57.
PB
4
16 tháng 9 2018
71 + 72 + 73 + 74 + 75 + 76 + 77 + 78 + 79
= ( 71 + 79 ) + ( 72 + 78 ) + ( 73 + 77 ) + ( 74 + 76 ) + 75
= 150 + 150 + 150 + 150 + 75
= 150 x 4 + 75
= 600 + 75
= 675
Tìm x :
X x 7 + X x 2 = 108
X x ( 7 + 2 ) = 108
X x 9 = 108
X = 108 : 9
X = 12
16 tháng 9 2018
\(71+72+73+74+75+76+77+78+79\)
\(=\left(71+79\right)+\left(72+78\right)+\left(73+77\right)+\left(74+76\right)+75\)
\(=150+150+150+150+75\)
\(=600+75\)
\(=675\)
\(X\)x\(7+X\)x\(2=108\)
\(X\)x\(\left(7+2\right)=108\)
\(X\)x\(9=108\)
\(X=108:9\)
\(X=12\)
Vậy \(X=12\)
NP
1
10 tháng 6 2016
Bài 71 :
Tam giác AHB = tam giác CKA ( c . g . c )
=> AB = CA , tam giác BHA = tam giác ACK
Ta lại có : Tam giác ACK + tam giác CAK = 90 độ
Nên tam giác BAH + tam giác CAK = 90 độ
Do đó tam giác BAC = 90 độ
Vậy tam giác ABC là tam giác vuông tại A
Bài 72
Xếp tam giác đều : Xếp tam giác với mỗi cạnh là bốn que diêm
Một tam giác cân mà ko đều : 2 cạnh bên 5 que diêm , cạnh đáy 2 que
Xét tam giác vuông : xếp tam giác có cạnh lần lượt là : ba , bốn , năm que diêm
Bài 73 ;
So sánh AC + CD vào 2 x BA
+ Xét tam giác AHB vuông tại H ,ta có :
AB2 = AH2 + HB2 ( định lý PItago )
=> HB2 =AB2 - AH2
=> HB2 = 5 - 3 = 25 - 9 =16 ( định lý Pitago )
=> HB= 4 ( vì HB > 0 )
+ Vì H nằm giữa B và C => :
HC = BC - HB = 10 - 4 = 6
+ Xét tam giác AHC vuông tại H , ta có
AC = AH + HC ( ĐỊNH LÝ PITAGO )
AC = 3 + 6 = 9 + 36 = 45
=> AC = 45 ( vì AC > 0 )
hay AC = 6,71
NT
2
10 tháng 1 2022
\(A=\left(1+7\right)+...+7^{2020}\left(1+7\right)=8\left(1+...+7^{2020}\right)⋮8\)
10 tháng 1 2022
\(A = (1 + 7) +...+7^2\)\(^0\)\(^2\)\(^0\) \((1 + 7) = 8 (1+...+7^2\)\(^0\)\(^2\)\(^0\)\() \) ⋮\(8\)
NQ
0
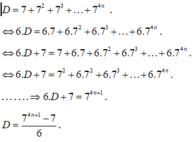
\(A=7+7+7^2+...+7^{100}\)
\(7A=7^2+7^2+7^3+...+7^{101}\)
\(A=14+7^2+7^{101}\)
Em xem thử lại đề bài nhé