Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC khi biết góc BAC bằng 120\(^\circ \).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 4 2023
a: Xét ΔABC vuông tại A có AH là đường cao
nên CA^2=CH*CB
b: \(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(AD=\dfrac{2\cdot15\cdot20}{15+20}\cdot cos45=\dfrac{60}{7}\sqrt{2}\)(cm)
AH=15*20/25=12(cm)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{12}{7}\left(cm\right)\)
c: ΔABI vuông tại A có AK là đường cao
nên BK*BI=BA^2=BH*BC
=>BK/BC=BH/BI
=>ΔBKH đồng dạng với ΔBCI
17 tháng 9 2023
a) I là giao điểm của ba đường phân giác tại ba góc A, B, C nên:
\(\widehat {IAB} = \widehat {IAC};\widehat {IBA} = \widehat {IBC};\widehat {ICB} = \widehat {ICA}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = 180^\circ \\\widehat {IAB} + \widehat {IAC} + \widehat {IBA} + \widehat {IBC} + \widehat {ICB} + \widehat {ICA} = 180^\circ \\2\widehat {IAB} + 2\widehat {IBC} + 2\widehat {ICA} = 180^\circ \end{array}\)
Vậy \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \).
b) Tổng ba góc trong một tam giác bằng 180°. Xét tam giác BIC:
\(\begin{array}{l}\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ \\\widehat {BIC} = 180^\circ - (\widehat {IBC} + \widehat {ICB})\end{array}\).
Mà \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \)→ \(\widehat {IBC} + \widehat {ICA} = 90^\circ - \widehat {IAB}\).
Vậy: \(\begin{array}{l}\widehat {BIC} = 180^\circ - (\widehat {IBC} + \widehat {ICB})\\\widehat {BIC} = 180^\circ - (90^\circ - \widehat {IAB})\\\widehat {BIC} = 90^\circ + \widehat {IAB}\end{array}\)
Mà \(\widehat {IAB} = \dfrac{1}{2}\widehat {BAC}\)(IA là phân giác của góc BAC).
Vậy \(\widehat {BIC} = 90^\circ + \widehat {IAB} = 90^\circ + \dfrac{1}{2}\widehat {BAC}\).
31 tháng 10 2021
\(a,\widehat{BIC}=180^0-\widehat{IBC}-\widehat{ICB}=180^0-\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)=180^0-\dfrac{1}{2}\left(180^0-\widehat{BAC}\right)=180^0-\dfrac{1}{2}\cdot100^0=130^0\)
CM
9 tháng 8 2018
Trong ΔBIC có: ∠(BIC) + ∠B1 + ∠C1 = 180o (tổng 3 góc trong tam giác)
Suy ra: ∠B1 + ∠C1 = 180o - ∠(BIC)
Ta có:
∠B1 = 1/2 ∠B (vì BD là tia phân giác)
∠C1 = 1/2 ∠C (vì CE là tia phân giác)
Suy ra: ∠B + ∠C = 2(∠B1 + ∠C1) = 2.(180o - ∠(BIC))
Trong ΔABC có: ∠A + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Suy ra: ∠A = 180o - (∠B + ∠C) = 180o - 2.(180o - ∠(BIC)) = 2. ∠(BIC) – 180o
∠(BIC) = 120o thì ∠A = 2.120o – 180o = 60o.
CM
28 tháng 4 2019
Trong ΔBIC có: ∠(BIC) + ∠B1 + ∠C1 = 180o (tổng 3 góc trong tam giác)
Suy ra: ∠B1 + ∠C1 = 180o - ∠(BIC)
Ta có:
∠B1 = 1/2 ∠B (vì BD là tia phân giác)
∠C1 = 1/2 ∠C (vì CE là tia phân giác)
Suy ra: ∠B + ∠C = 2(∠B1 + ∠C1) = 2.(180o - ∠(BIC))
Trong ΔABC có: ∠A + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Suy ra: ∠A = 180o - (∠B + ∠C) = 180o - 2.(180o - ∠(BIC)) = 2. ∠(BIC) – 180o
∠(BIC) = α thì ∠A = 2.α – 180o.
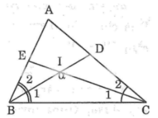
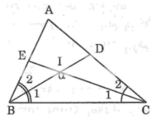
Vì BI là tia phân giác của góc ABC nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)
Vì CI là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \\ \Rightarrow \widehat {ABC} + \widehat {ACB} = 180^\circ - \widehat {BAC} = 180^\circ - 120^\circ = 60^\circ \\ \Rightarrow \widehat {{B_2}} + \widehat {{C_2}} = \dfrac{1}{2}.\left( {\widehat {ABC} + \widehat {ACB}} \right) = \dfrac{1}{2}.60^\circ = 30^\circ \end{array}\)
Áp dụng định lí tổng ba góc trong tam giác BIC, ta có:
\(\begin{array}{l}\widehat {BIC} + \widehat {{B_2}} + \widehat {{C_2}} = 180^\circ \\ \Rightarrow \widehat {BIC} = 180^\circ - \left( {\widehat {{B_2}} + \widehat {{C_2}}} \right) = 180^\circ - 30^\circ = 150^\circ \end{array}\)
Vậy \(\widehat {BIC} = 150^\circ \)