Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

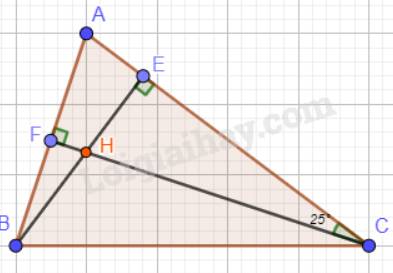
Xét tam giác AFC có: \(\widehat {HCA} = 25^\circ \); \(\widehat {AFC} = 90^\circ \) (vì CF vuông góc với AB).
Nên: \(\widehat {FAC} = \widehat {BAC} = 90^\circ - 25^\circ = 65^\circ \).
Xét tam giác AEB có: \(\widehat {BAC} = 65^\circ \); \(\widehat {AEB} = 90^\circ \)(vì BE vuông góc với AC).
Nên: \(\widehat {ABE} = \widehat {HBA} = 90^\circ - 65^\circ = 25^\circ \).

nhanh lên mình cần gấp lắm
giúp mình với huhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhu

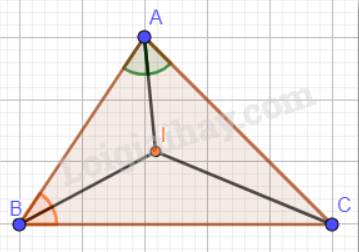
Ta có: I là giao điểm của hai đường phân giác góc A và góc B nên suy ra: CI là đường phân giác của góc C.
Vậy \(\widehat {ICA} = \widehat {ICB}\) ( tính chất tia phân giác của một góc).
Đáp án: A. \(\widehat {ICA} = \widehat {ICB}\).

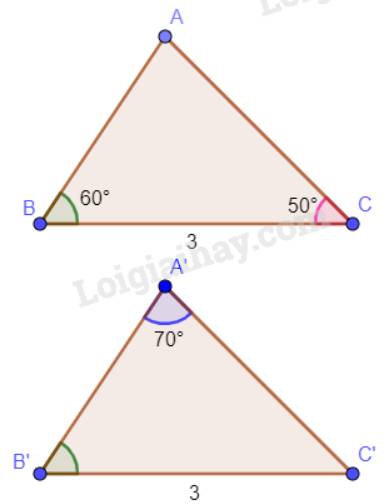
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)

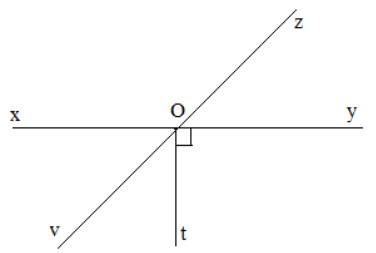
Vì \(\widehat {yOt} = 90^\circ \Rightarrow Oy \bot Ot \Rightarrow Ox \bot Ot\) nên \(\widehat {xOt} = 90^\circ \)
Vì Ov là tia phân giác của \(\widehat {xOt}\) nên \(\widehat {xOv} = \widehat {vOt} = \frac{1}{2}.\widehat {xOt} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì \(\widehat {vOz} =\widehat {vOx} + \widehat {xOz} = 45^\circ + 135^\circ = 180^\circ \) nên Ov và Oz là hai tia đối nhau
Như vậy, các góc \(\widehat {xOv}\) và \(\widehat {yOz}\) là hai góc đối đỉnh vì Ox là tia đối của tia Oy, tia Ov là tia đối của tia Oz

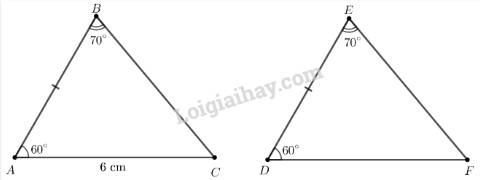
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}\widehat {ABC} = \widehat {DEF} (= {70^\circ })\\AB = DE\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)
\( \Rightarrow \Delta ABC{\rm{ = }}\Delta DEF\)(g.c.g)
\( \Rightarrow DF = AC\)( 2 cạnh tương ứng)
Mà AC = 6 cm
\( \Rightarrow DF = 6cm\)

a) I là giao điểm của ba đường phân giác tại ba góc A, B, C nên:
\(\widehat {IAB} = \widehat {IAC};\widehat {IBA} = \widehat {IBC};\widehat {ICB} = \widehat {ICA}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = 180^\circ \\\widehat {IAB} + \widehat {IAC} + \widehat {IBA} + \widehat {IBC} + \widehat {ICB} + \widehat {ICA} = 180^\circ \\2\widehat {IAB} + 2\widehat {IBC} + 2\widehat {ICA} = 180^\circ \end{array}\)
Vậy \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \).
b) Tổng ba góc trong một tam giác bằng 180°. Xét tam giác BIC:
\(\begin{array}{l}\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ \\\widehat {BIC} = 180^\circ - (\widehat {IBC} + \widehat {ICB})\end{array}\).
Mà \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \)→ \(\widehat {IBC} + \widehat {ICA} = 90^\circ - \widehat {IAB}\).
Vậy: \(\begin{array}{l}\widehat {BIC} = 180^\circ - (\widehat {IBC} + \widehat {ICB})\\\widehat {BIC} = 180^\circ - (90^\circ - \widehat {IAB})\\\widehat {BIC} = 90^\circ + \widehat {IAB}\end{array}\)
Mà \(\widehat {IAB} = \dfrac{1}{2}\widehat {BAC}\)(IA là phân giác của góc BAC).
Vậy \(\widehat {BIC} = 90^\circ + \widehat {IAB} = 90^\circ + \dfrac{1}{2}\widehat {BAC}\).