Cho \(C = f\left( d \right)\)là hàm số mô tả mối quan hệ giữa chu vi \(C\) và đường kính \(d\) của một đường tròn. Tìm công thức \(f\left( d \right)\) và lập bảng giá trị của hàm số ứng với \(d\) lần lượt bằng \(1;2;3;4\) (theo đơn vị cm).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
11 tháng 9 2023
a) Đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ xác nhận được duy nhất một giá trị \(y\) tương ứng.
b) \(f\left( 2 \right) = {2^2} = 4;f\left( { - 3} \right) = {\left( { - 3} \right)^2} = 9\)
Ta có: \(f\left( { - 2} \right) = {\left( { - 2} \right)^2} = 4;f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\(f\left( 0 \right) = {0^2} = 0;f\left( 1 \right) = {1^2} = 1\)
\(f\left( 2 \right) = {2^2} = 4;f\left( 3 \right) = {3^2} = 9\)
\(x\) | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
\(f\left( x \right)\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
HQ
Hà Quang Minh
Giáo viên
11 tháng 9 2023
a) \(f\left( 1 \right) = 3.1 = 3;f\left( { - 2} \right) = 3.\left( { - 2} \right) = - 6;f\left( {\dfrac{1}{3}} \right) = 3.\dfrac{1}{3} = 1\).
b) Ta có: \(f\left( { - 3} \right) = 3.\left( { - 3} \right) = - 9;f\left( { - 1} \right) = 3.\left( { - 1} \right) = - 3\)
\(f\left( 0 \right) = 3.0 = 0;f\left( 2 \right) = 3.2 = 6;f\left( 3 \right) = 3.3 = 9\);
Ta lập được bảng sau
\(x\) | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
\(y\) | –9 | -6 | –3 | 0 | 3 | 6 | 9 |
HQ
Hà Quang Minh
Giáo viên
12 tháng 9 2023
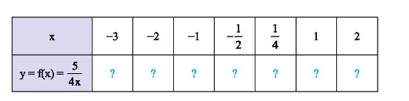
a) Ta có:
\(f\left( {\dfrac{1}{5}} \right) = \dfrac{5}{{4.\dfrac{1}{5}}} = \dfrac{5}{{\dfrac{4}{5}}} = 5:\dfrac{4}{5} = 5.\dfrac{5}{4} = \dfrac{{25}}{4};\)
\(f\left( { - 5} \right) = \dfrac{5}{{4.\left( { - 5} \right)}} = \dfrac{5}{{ - 20}} = \dfrac{{ - 1}}{4};\)
\(f\left( {\dfrac{4}{5}} \right) = \dfrac{5}{{4.\dfrac{4}{5}}} = \dfrac{5}{{\dfrac{{16}}{5}}} = 5:\dfrac{{16}}{5} = 5.\dfrac{5}{{16}} = \dfrac{{25}}{{16}}\)
b) Ta có:
\(f\left( { - 3} \right) = \dfrac{5}{{4.\left( { - 3} \right)}} = \dfrac{5}{{ - 12}} = \dfrac{{ - 5}}{{12}};\)
\(f\left( { - 2} \right) = \dfrac{5}{{4.\left( { - 2} \right)}} = \dfrac{5}{{ - 8}} = \dfrac{{ - 5}}{8};\)
\(f\left( { - 1} \right) = \dfrac{5}{{4.\left( { - 1} \right)}} = \dfrac{5}{{ - 4}} = \dfrac{{ - 5}}{4};\)
\(f\left( { - \dfrac{1}{2}} \right) = \dfrac{5}{{4.\left( { - \dfrac{1}{2}} \right)}} = \dfrac{5}{{\dfrac{{ - 4}}{2}}} = \dfrac{5}{{ - 2}} = \dfrac{{ - 5}}{2}\);
\(f\left( {\dfrac{1}{4}} \right) = \dfrac{5}{{4.\dfrac{1}{4}}} = \dfrac{5}{{\dfrac{4}{4}}} = \dfrac{5}{1} = 5\);
\(f\left( 1 \right) = \dfrac{5}{{4.1}} = \dfrac{5}{4}\);
\(f\left( 2 \right) = \dfrac{5}{{4.2}} = \dfrac{5}{8}\)
Ta có bảng sau:
\(x\) | –3 | –2 | –1 | \( - \dfrac{1}{2}\) | \(\dfrac{1}{4}\) | 1 | 2 |
\(y = f\left( x \right) = \dfrac{5}{{4x}}\) | \(\dfrac{{ - 5}}{{12}}\) | \(\dfrac{{ - 5}}{8}\) | \(\dfrac{{ - 5}}{4}\) | \(\dfrac{{ - 5}}{2}\) | 5 | \(\dfrac{5}{4}\) | \(\dfrac{5}{8}\) |
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Thay \(x = - 3\) vào hàm số ta được:
\(y = {\left( { - 3} \right)^2} + 2.\left( { - 3} \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Thay \(x = - 2\) vào hàm số ta được:
\(y = {\left( { - 2} \right)^2} + 2.\left( { - 2} \right) - 3 = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = - 1\) vào hàm số ta được:
\(y = {\left( { - 1} \right)^2} + 2.\left( { - 1} \right) - 3 = - 4\). Điền \( - 4\) vào ô tương ứng.
Thay \(x = 0\) vào hàm số ta được:
\(y = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = 1\) vào hàm số ta được:
\(y = {\left( 1 \right)^2} + 2.\left( 1 \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Vậy ta có:
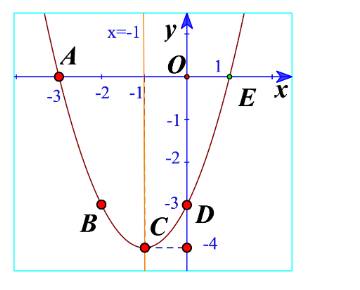
b) Các điểm có trong hình 11.
c) Đường cong đi qua 5 điểm là parabol trong hình 11.
d) Từ đồ thị ta thấy điểm thấp nhất là điểm C(-4;-1)
Phương trình trục đối xứng là x=-1
Đồ thị có bề lõm lên trên.
4 tháng 4 2017
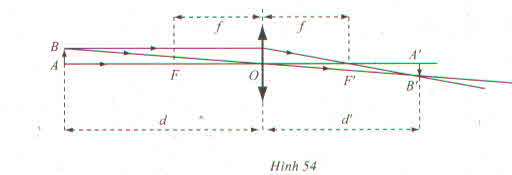
a) Từ hệ thức suy ra d' = φ(d) =
.
b) +) φ(d) =
= +∞ .
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực.
+) φ(d) =
= -∞.
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô sực.
+) φ(d) =
=
= f.
Ý nghĩa: Nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính).
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 4 2021
1.
\(f'\left(x\right)=3x^2-6mx+3\left(2m-1\right)\)
\(f'\left(x\right)-6x=3x^2-3.2\left(m+1\right)x+3\left(2m-1\right)>0\)
\(\Leftrightarrow x^2-2\left(m+1\right)x+2m-1>0\)
\(\Leftrightarrow x^2-2x-1>2m\left(x-1\right)\)
Do \(x>2\Rightarrow x-1>0\) nên BPT tương đương:
\(\dfrac{x^2-2x-1}{x-1}>2m\Leftrightarrow\dfrac{\left(x-1\right)^2-2}{x-1}>2m\)
Đặt \(t=x-1>1\Rightarrow\dfrac{t^2-2}{t}>2m\Leftrightarrow f\left(t\right)=t-\dfrac{2}{t}>2m\)
Xét hàm \(f\left(t\right)\) với \(t>1\) : \(f'\left(t\right)=1+\dfrac{2}{t^2}>0\) ; \(\forall t\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow f\left(t\right)>f\left(1\right)=-1\Rightarrow\) BPT đúng với mọi \(t>1\) khi \(2m< -1\Rightarrow m< -\dfrac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 4 2021
2.
Thay \(x=0\) vào giả thiết:
\(f^3\left(2\right)-2f^2\left(2\right)=0\Leftrightarrow f^2\left(2\right)\left[f\left(2\right)-2\right]=0\Rightarrow\left[{}\begin{matrix}f\left(2\right)=0\\f\left(2\right)=2\end{matrix}\right.\)
Đạo hàm 2 vế giả thiết:
\(-3f^2\left(2-x\right).f'\left(2-x\right)-12f\left(2+3x\right).f'\left(2+3x\right)+2x.g\left(x\right)+x^2.g'\left(x\right)+36=0\) (1)
Thế \(x=0\) vào (1) ta được:
\(-3f^2\left(2\right).f'\left(2\right)-12f\left(2\right).f'\left(2\right)+36=0\)
\(\Leftrightarrow f^2\left(2\right).f'\left(2\right)+4f\left(2\right).f'\left(2\right)-12=0\) (2)
Với \(f\left(2\right)=0\) thế vào (2) \(\Rightarrow-12=0\) ko thỏa mãn (loại)
\(\Rightarrow f\left(2\right)=2\)
Thế vào (2):
\(4f'\left(2\right)+8f'\left(2\right)-12=0\Leftrightarrow f'\left(2\right)=1\)
\(\Rightarrow A=3.2+4.1\)
Ta có: \(C = \pi .d\) trong đó, \(C\) là chu vi đường tròn; \(d\) là đường kính và \(\pi \) là số pi.
Do đó, \(f\left( d \right) = \pi .d\)
Với \(d = 1 \Rightarrow f\left( 1 \right) = \pi .1 = \pi \);
\(d = 2 \Rightarrow f\left( 2 \right) = \pi .2 = 2\pi \);
\(d = 3 \Rightarrow f\left( 3 \right) = \pi .3 = 3\pi \);
\(d = 4 \Rightarrow f\left( 4 \right) = \pi .4 = 4\pi \).
Ta thu được bảng sau:
\(d\)
1
2
3
4
\(f\left( d \right)\)
\(\pi \)
\(2\pi \)
\(3\pi \)
\(4\pi \)